クイズ:どっちが自然の構造? 〜RF diffusionで人工ペプチドを生成〜
毎年恒例、お正月の創薬ちゃんの創薬人格付けチェック。今年はタンパク質の複合体がお題でしたね。
元旦恒例 #創薬人格付けチェック!
— 叢雲くすり (創薬ちゃん) 💊LLM創薬チャレンジ開催中 (@souyakuchan) 2023年1月1日
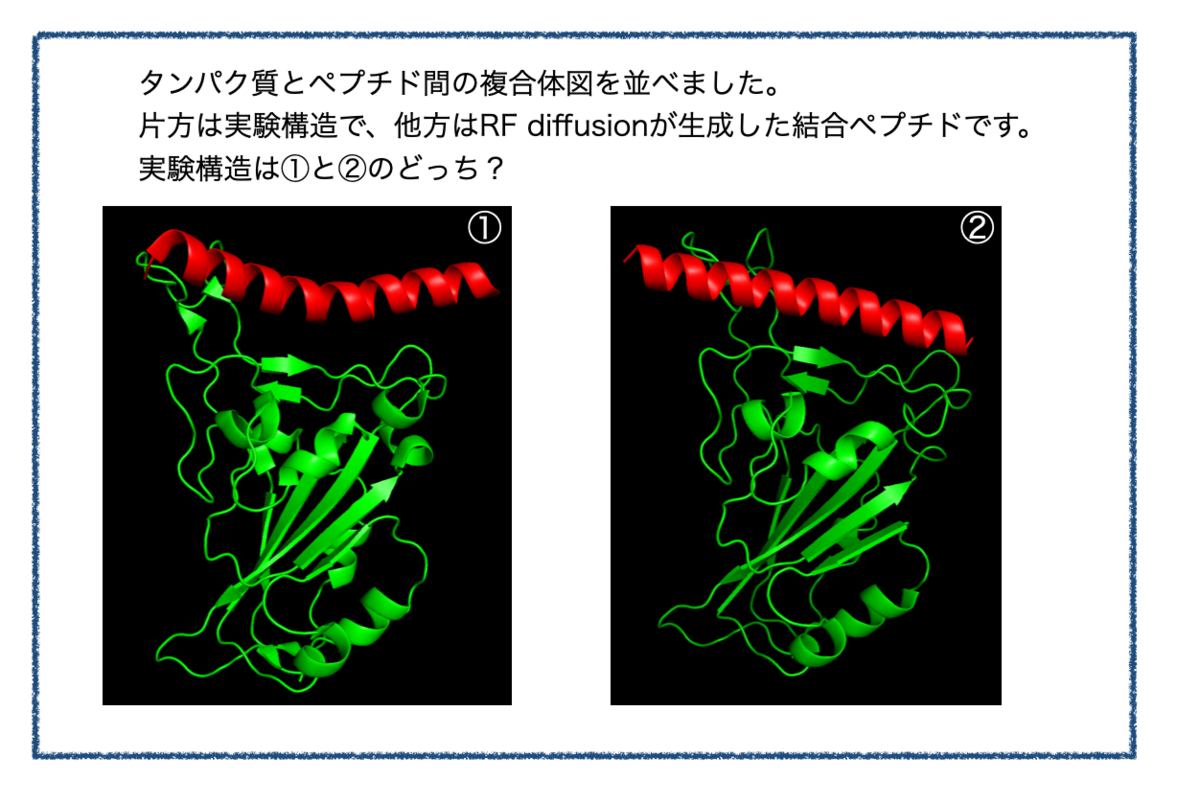
今回はタンパク質–ペプチド間相互作用。動画(平行法ステレオ図)に示す2つの結合構造のうち、片方が正解構造、もう片方はAlphaFold2が生成したまことしやかな幻だ。
正しいと思うのはどちらだろうか? 次のツイートで投票を取る。#souyakuchan_quiz#格付けチェック pic.twitter.com/AtAHShY9rG
アンケート結果を見てAlphaFold2の幻を見破った方が多いのにびっくりしました。創薬ちゃんフォロワーのレベル高い。。。
さらなる高みをめざし、続問をつくってみました!
- ムービー
- きっかけ
- お題のタンパク質
- Google ColabでRF diffusion(hotspot指定なし)
- Google ColabでRF diffusion(hotspot指定あり)
- 答え
- ProteinMPNNによる残基の生成とAlphaFoldでの検証
- まとめ
ムービー
GIFも貼っときます。
① 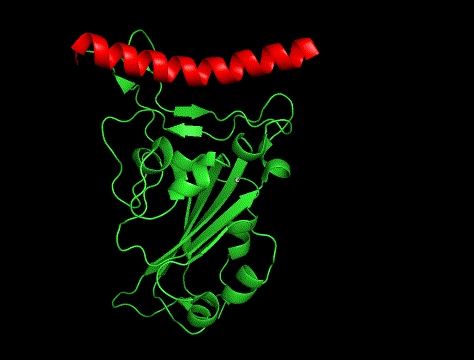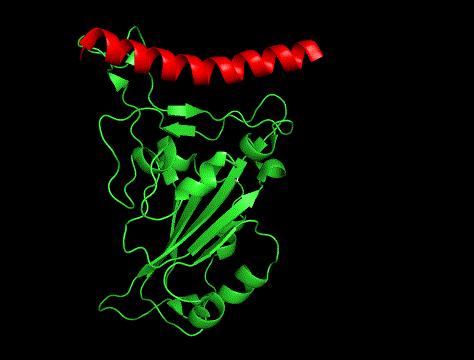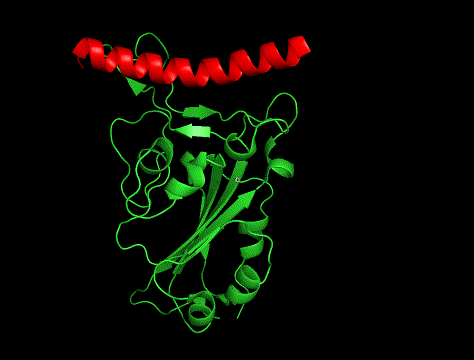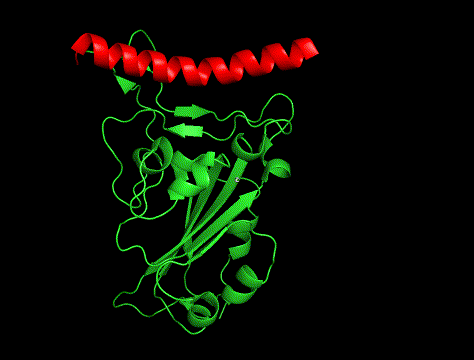
② 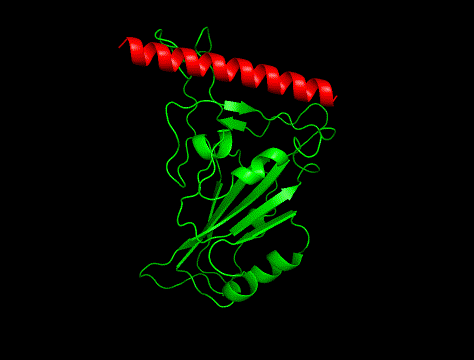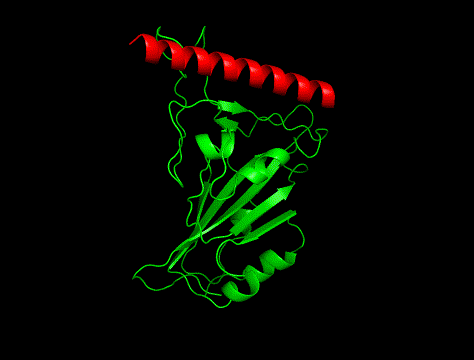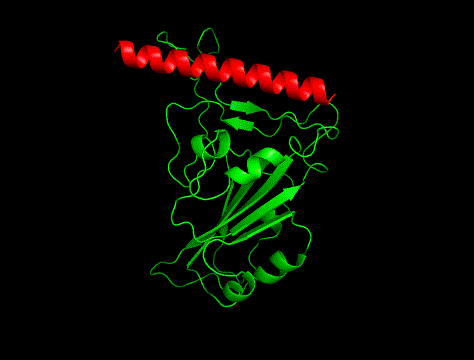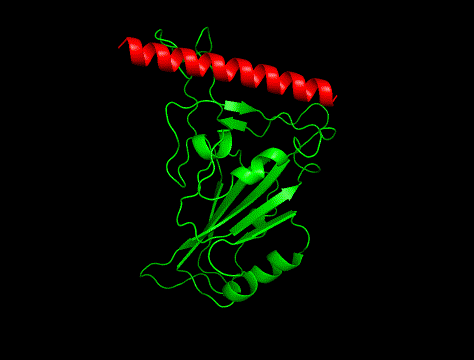
きっかけ
LabCodeさんのブログ記事でRF Diffusionというのを知りました。
Baker Labで開発された技術で、標的のタンパク質構造に対して結合するペプチドをつくってくれるそうです。すごい。
これで新しいペプチドを作ったら、自然界の構造と見分けられるのだろうか?
Twitterのプロたちは見分けるに違いない!
お題のタンパク質
標的タンパク質は格付けチェックにあわせてSARS-CoV-2 Spikeタンパク質の受容体結合ドメイン(RBD)としました。
進化的に獲得され保存されている相互作用様式に該当しないような MSA の薄いものにはまだ AF2 も弱いということかもしれない。今回の出題は SARS-CoV-2 Spike RBD と ACE2 の RBD 結合モチーフ部分であり、つまり自然界で最近たまたま出会ってたまたま結合したものに相当する。 pic.twitter.com/hRxwCg2TQp
— 叢雲くすり (創薬ちゃん) 💊LLM創薬チャレンジ開催中 (@souyakuchan) 2023年1月22日
自然界の結合相手としてACE2のRBD結合モチーフが知られているそうです。
複合体のX線結晶構造解析としては「PDB ID: 6M0J」などがありました。

論文はこちら
相互作用がある残基はExtended Data Table 2にまとめられています。
PyMolで描画だ!

チロシンが複数あって目にとまりますが、疎水性相互作用というよりも水素結合を結構作っているみたいです。ほー。
Google ColabでRF diffusion(hotspot指定なし)
ではRBDに結合するペプチドをつくってみましょう!
LabCodeさんの先のブログ記事に丁寧に解説してくださっていますので、手順はそちらをご参照ください。
Google Colabでノートブックにアクセスしてボタンを押すだけです。
元の構造には「PDB="6M0J"」を使いました。
このうち結合対象は「E鎖」で、生成するペプチドの長さを「30」としました。これらはcontigsという設定項目に記載するそうなので「contigs="E:30"」としました。
ペプチド生成の様子をアニメーションにすることができます。

おー!!すごい。
・・・でも結合して欲しい箇所そこじゃない。上の方のループと結合して欲しいのに。。。
Google ColabでRF diffusion(hotspot指定あり)
RF diffusionにはhotspotという設定項目もあり、ここに結合して欲しい箇所の残基を入力することで、結合ペプチドの生成対象箇所を絞り込めるようです。
さきの文献のTable 1を参考にスパイクタンパク RBDの残基を指定してみます。少し数が多いですがE鎖の残基番号をつかって「hotspot = "E417,E446,E449,E487,E489,E493,E500,E501,E502,E505"」 としました。
もう一回ペプチドを生成だ!

今回はちゃんと図の上側を対象に生成されているようです。
さきほどのアニメーションよりもすぐに構造ができているので構造生成感は低めですが、ヘリックス構造が瞬時に構築されているのは驚きです。
答え
冒頭の画像比較につかっているのは「hotspot指定あり」で生成した構造でした。
「①と②のどちらが正解か?」をみるまえに、まず実験構造(PDB : 6M0J)から結合位置のみを切り取った構造を描画してみます。
こんな感じ。

ACE2のRBD結合箇所もヘリックス(赤色)で、ポケットに合わせてか、少し湾曲しています。
一方、RF Diffusionで出てきたペプチド骨格はこんな感じ。
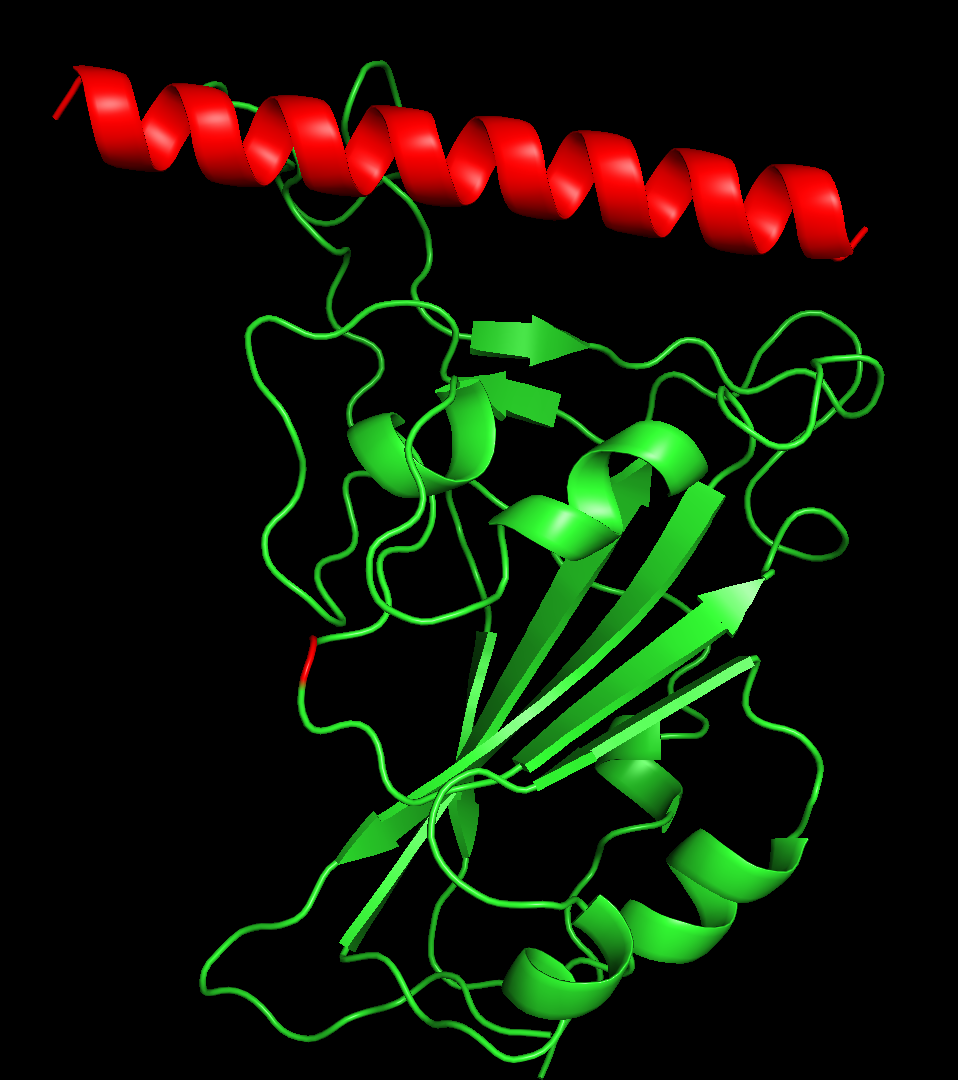
ヘリックスが真っ直ぐ!
というわけで、実験構造は①でした。
ProteinMPNNによる残基の生成とAlphaFoldでの検証
クイズはおしまいですが、ペプチド生成には続きがあります。
RF diffusionで出てくるのは骨格のみです。実際に、先のRF diffusionで出てくる構造では残基がすべてグリシン(G)となっていました。
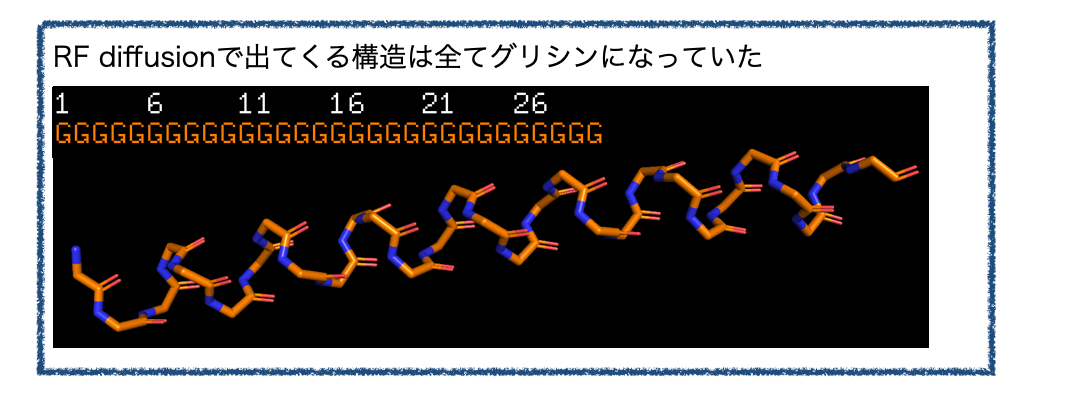
もっと具体的なペプチドにするにはProteinMPNNというソフトで骨格に合わせた残基を生成し、生成した残基から再度AlphaFold2で立体構造を予測して望みの構造になっているか検証する必要があるそうです。
これらの工程も同じGoogle Colabのノートブックに用意されているのでそのまま実行してみましょう!
生成した構造はPDBファイルとしてダウンロードできます。一押しの構造は「best.pdb」というファイル名になっていました。
ベストはこれだ!

いろいろな残基をくみあわせたヘリックス構造になっています。リシン(K)とグルタミン酸(E)が多めでしょうか?
複合体として描画してみましょう。

さっきと結合位置がかわってる???
残念ながらAlphaFoldによる検証では、予測された複合体の構造が望みのものとは異なりました。・・・残念。
まとめ
というわけで、今回はRF diffusionで創薬ちゃん格付けチェックの続編を(勝手に)つくってみました。
すんなりとヘリックス構造がでてきてびっくりしました。構造生成のアニメーションも格好いいです。
面白かった点として、「hotspotを指定しない」場合にはRBDのループと反対側(図下側)を対象にペプチドが生成されたこと、「hotspotを指定して」骨格を作った場合でもProteinMPNNを経たAlphaFoldの検証では異なる結合位置となっていたことがあります。
創薬ちゃんのクイズを見返してみると、AlphaFoldによる幻はRBDのループと反対側に対して結合するように予測されているように見えます。「hotspotを指定しない」場合に似ていますね。
スパイクタンパク質全体の一部(RBDのみ)を切り取った構造を対象にしているから生じた問題かもしれませんが、AlphaFoldによる複合体予測の癖(?)が垣間見えるようで面白いですね。
ではでは!
ニューモダリティはあなたの中に? 〜FMTが承認された話〜
あけましておめでとうございます。本年もどうぞよろしくお願い申し上げます。
早速ですが・・・
「モダリティって200種類あんねん」
と、いうわけで、新年初記事は、昨年末FDAに初めて承認されたモダリティFMTについて取り上げたいと思います。
注)お食事中には読まないでね!

注) この記事には医療に関わる内容を含みますが私は医療従事者・専門家ではありません。正しさを保証できませんのでご留意ください。
初のFMT、Rebyota
FMTとはFecal Microbiota Transplantation(糞便移植、便微生物移植)の略です。日本語で書くとなかなかインパクトのある名前ですね。
おおざっぱにいうと「健康なヒトの腸内細菌叢(microbiota)を患者さんに移植して疾患を治療しよう!」ってやつです。
初めて聞くと「ウソやん・・・」って感じですが、れっきとした治療法で、昨年末、FDAより初の糞便細菌叢製剤であるRebyotaが承認されました。
- FDA Approves First Fecal Microbiota Product (FDA News Release, November 30, 2022)
適応はクロストリジオイデス・ディフィシル感染症(Clostridioides difficile infection、CDI)の再発予防です。
Rebyota(RBX2660)はもともとマイクロバイオームに焦点を当てて医薬品開発を行っているRebiotix社により開発されていましたが、現在は買収されFerring Pharmaceuticalsの傘下となっているようです。*2
CDIってどんな?
さて、Rebyotaの適応となっているCDIとはどのような疾患なのでしょうか?
MSDマニュアル(家庭版)「クロストリジオイデス・ディフィシャル腸炎」などを参考に、かいつまんで見るとこんな感じ。

抗菌薬によるディスバイオーシスで、特定の細菌が増えることでおこる感染症のようです。このCDIが重度で再発が続くことがあるらしく、これがRebyotaの適応症です。
承認時のFDA News Release(前掲)によると、アメリカではCDIに関連する死者が年間15,000 ~ 30,000人となっているそうです。こんなに深刻なものとは全く知りませんでした。
Rebyota の有効性について
では実際にRebyotaの有効性はどのようなものだったのでしょうか?
Ferringa社より公開されている添付文書を参照してみます。(添付文書PDF)

ベイズ解析の結果、8週の盲検化治療後の推定治療成功率がREBYOTA群(70.6%)、プラセボ群(57.5%)であり、13.1%の差があったそうです。これはREBYOTAがプラセボよりも優れている事後確率(Posterior Probability of Superiority)99.1%に相当し、あらかじめ定義されていた閾値(Pre-defined threshold)97.5%を上回るものでした。
・・・さっぱりわかりません。多分効いてる。。。
Phase IIIの臨床試験の論文も公開されているようなので、詳しい方説明してください。(オープンアクセス、CC BY-NC 4.0)
Khanna, S., Assi, M., Lee, C. et al. Efficacy and Safety of RBX2660 in PUNCH CD3, a Phase III, Randomized, Double-Blind, Placebo-Controlled Trial with a Bayesian Primary Analysis for the Prevention of Recurrent Clostridioides difficile Infection. Drugs 82, 1527–1538 (2022). https://doi.org/10.1007/s40265-022-01797-x
それっぽいのだけ引用しておきます。6ヶ月間続けて追いかけた時のCDI再発のカプラン・マイヤー分析です。

プラセボよりREBYOTA(RBX2660)群の方が再発率が低いままのようですね。
Rebyotaだけじゃないよ!
さて、ざっとRebyotaについて見てきましたが、マイクロバイオームを利用した創薬には他にどんなものがあるのでしょうか?
まずは同じCDI再発抑制を目的としたFMTとして、経腸製剤であるRebyotaに対して、経口製剤であるRBX7455(Rebiotix社, Ferring社)やSER-109(Seres Therapeutics)などが現在臨床開発中のようです。後者にはNestleも開発に関わっているそう。なかなか興味深い取り組みですね。
また、FMTの他にLBPs(Live Biotherapeutic Products)というものもあるそうです。FMTでは「どの菌種が疾患の治療に効果があるのか不明」なのに対して、LBPsでは「着目すべき菌種を同定し、単一ないし複数種の腸内細菌製剤」を用いるという違いがあります。
CDI再発抑制を適応としたLBPsもあり、Vedanta BiosciencesのVE303や、Finch TherapeuticsのCPT101といった開発品があるそうです。
まとめと参考資料
以上、今回は新年に相応しく(?)、最近承認された新しいモダリティとしてFMTをとりあげてみました。専門外すぎて雑な記事ですみません。
マイクロバイオームの医療への応用としては、他にもさまざま疾患があり、また治療だけでなくバイオマーカーとして診断に利用する取り組みもあります。以下の日本語資料がわかりやすくおすすめです*3。
- 独立行政法人 医薬品医療機器総合機構(PMDA) 科学委員会専門部会 マイクロバイオーム専門部会
「マイクロバイオーム研究に基づいた細菌製剤に関する報告書」
(右ページにてPDFを閲覧可:議論の取りまとめ報告書) - 医薬産業政策研究所 政策研ニュース No.67 2022年11月発行
「 新モダリティの開発動向調査 -mRNAとマイクロバイオーム- 」
医薬産業政策研究所 主任研究員 高橋洋介 氏による記事
不勉強でよく知らなかった分野ですが、門外漢でもこの数年で目にする機会がぐっと増えた腸内細菌に関する創薬。承認され実用化されるまで進んでいるとは知りませんでした。技術の発展はすごいですね。
正直、「糞便移植」という言葉を初めて知った時はちょっと抵抗感を感じてしまいましたが、人体に共生しているシステムを利用してバランスを取り戻すという点ではとても興味深いです。
ところで昨年は本当に今は2020年代なのかとちょっと目を疑うようなニュースが多かったです。ちょっとディスバイオシス感ある世の中に一刻も早くバランスが戻るといいですね。
・・・上手くまとめられなかった。
今回も色々と間違いが多いと思います。ご指摘いただけると嬉しいです。ではでは!
静電ポテンシャルからタンパク質-リガンド複合体を眺めよう 〜パート②:Tyk2阻害剤への適用
リガンド-タンパク質複合体を静電ポテンシャル図で眺める記事の後編です。前編で使い方をお勉強したESP-DNNを実際のより複雑な例に適用してみましょう!
計算対象としては②TYK2キナーゼ阻害剤 (ΔG_expデータセット)を用います。

1. 計算対象
1-1. Tyk2キナーゼ阻害剤データセット
今回取り上げる例はTYK2キナーゼ阻害剤(ΔG_expデータセット)です。
自由エネルギーとリガンド結合親和性との関係に焦点をあてたデータセットで、もともとは以下の文献に由来するもののようです。
Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field
J. Am. Chem. Soc. 2015, 137, 7, 2695–2703
自由エネルギー計算の分野では有名なものらしく、Open Force Fieldのベンチマーク(protein-ligand-benchmark)にも含まれています。
また、機械学習を自由エネルギー計算に応用した下記プレプリントでも対象として取り上げられています。(bioRxiv, CC-BY 4.0)
- 日本語解説:Preferred Netowrks Blog Neural Network Potentialを用いたタンパク-薬剤結合自由エネルギー計算の改善
具体的には以下のようなキナーゼ阻害剤化合物とデータです。*1
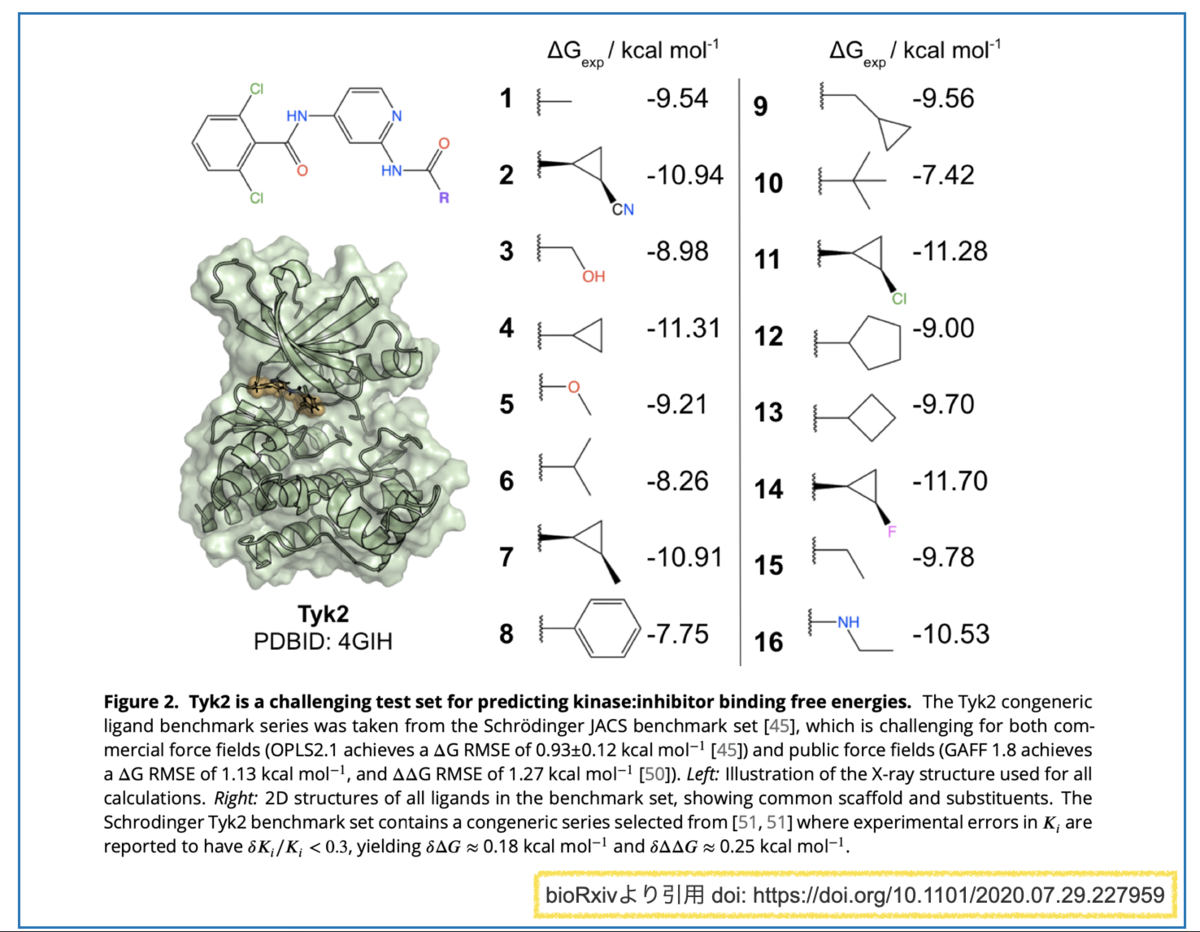
共通の骨格を有し、Rグループが異なる化合物群です。それぞれについて結合親和性のエネルギー(ΔG_exp)が求められています。
置換基の構造で「-7.4 kcal/mol ~ -11.7 kcal/mol」と広い幅で親和性が変化していてとても興味深いですね。
この活性の差を静電ポテンシャルで考察できたら面白そう!!!
1-2. データセットの取得元と変換
さて、Tyk2キナーゼ阻害剤データセットの化合物構造ですが、今回はOpen Force FieldのGitHubに格納されているものを利用させていただくことにしました。*2
上記にタンパク質(pdb)およびリガンドの構造データ(sdf)が含まれています。
注意点として、ESP-DNNの対応入力ファイルはPDBです。そこでリガンドデータをRDKitでそれぞれPDBに変換して用いました。
from rdkit import Chem m = Chem.SDMolSupplier("lig_ejm_54.sdf")[0] mH = Chem.AddHs(m, addCoords=True) Chem.MolToPDBFile(mH, "lig_ejm_54.pdb")
リガンドのsdfファイルは一つずつ別々のディレクトリに入っています。以下の図に構造とGitHubのディレクトリ名との対応を書いたのでご参考までに。。。
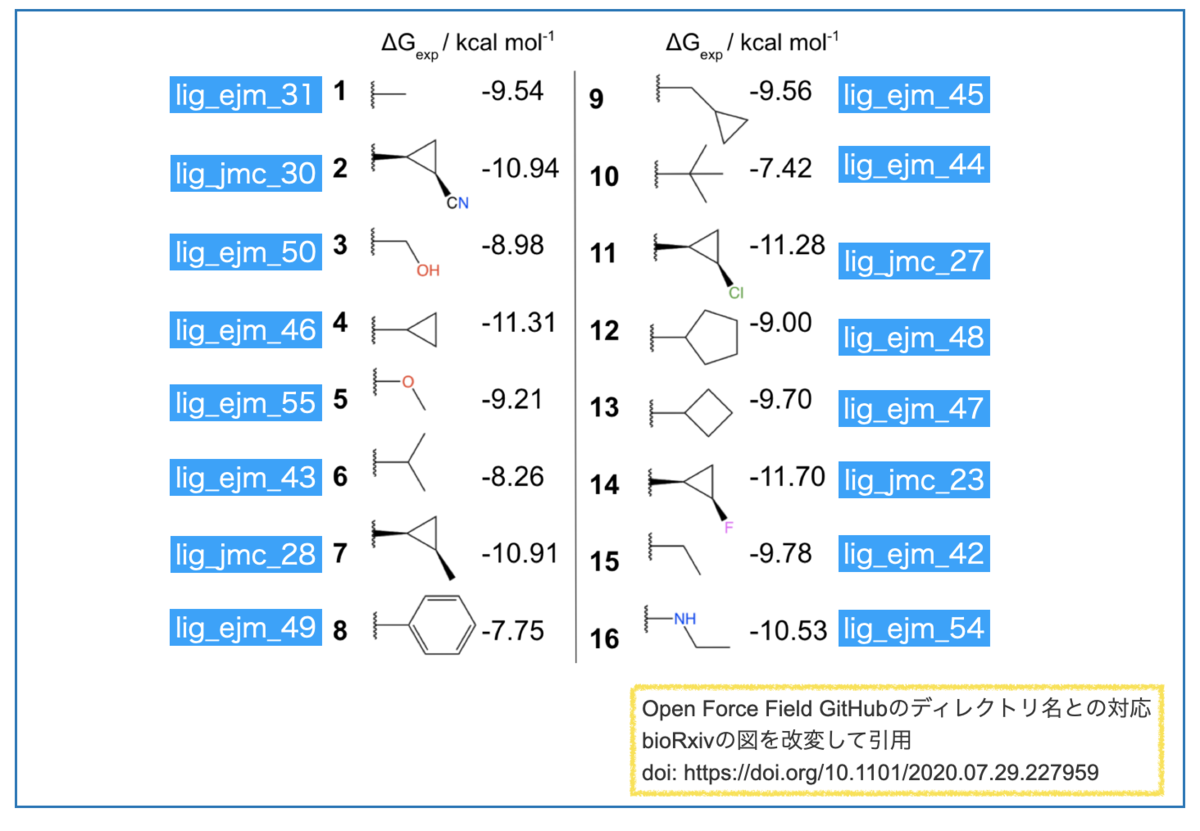
以上が今回の計算対象とデータの取得元です。
2. ESPを計算して活性差を考察しよう
2-1. 計算対象の絞り込みと傾向
「早速計算してみよう!」といきたいところですが、テーブルの化合物数がそこそこ多いです(16個)。
そこで、データセットの中でも構造が似通ったシクロプロピル基を持つもののみに注目してみます(下図、青枠)。
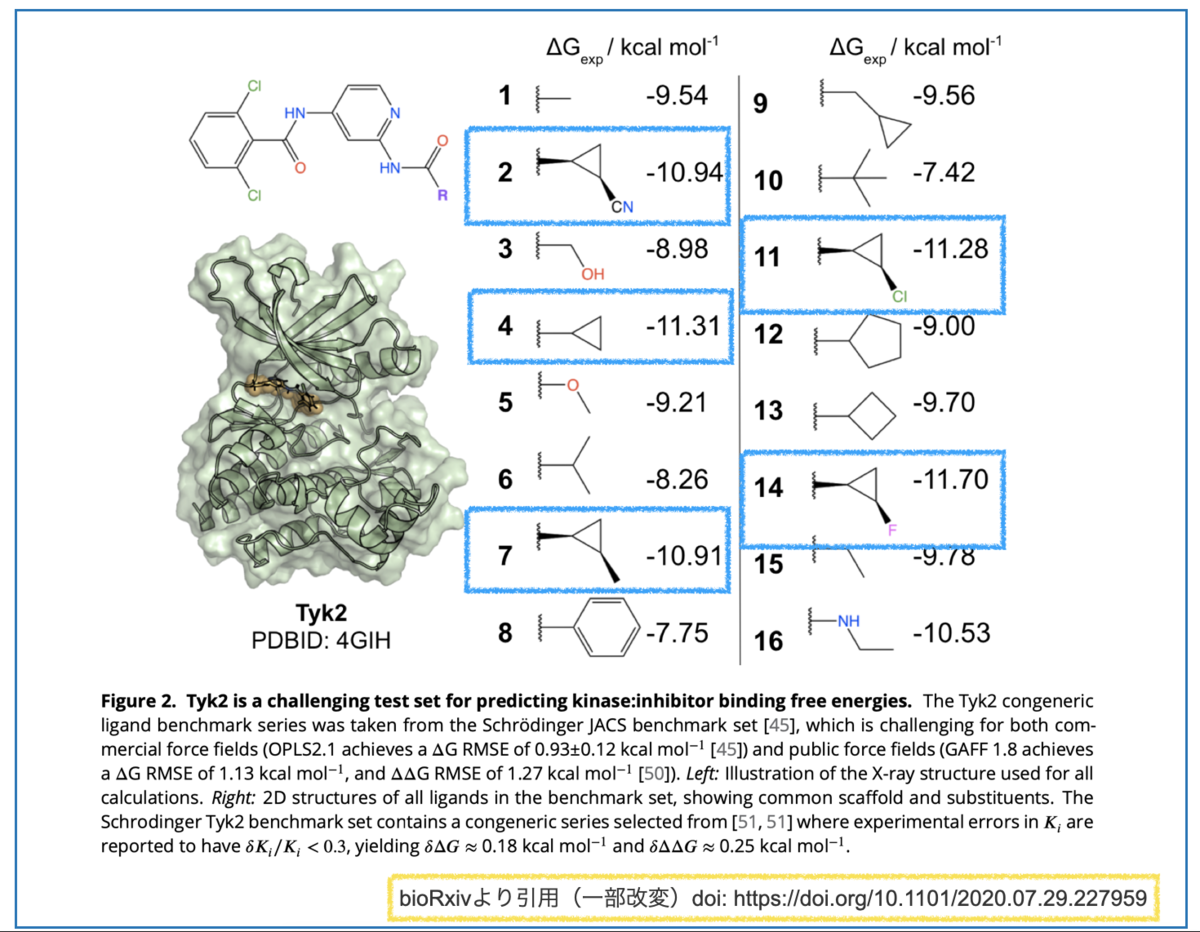
F置換(14)> 無置換(4)~ Cl置換(11) > CN置換(2)~ メチル置換(7)の順に活性が下がっています。
電子求引基の方が活性が良さそう(F vs. H, Cl > Me)ですが、大きくなると活性に悪そうです(H > CN, Me)。
2-2. PyMolで眺める
2次元の構造式で見た傾向が3次元ではどうなるか?PyMolで描画してみました。

複合体図の下半分はシクロプロピル基周辺の拡大です。近接するアミノ酸残基「Tyr、Arg、Leu」をSpheres表示にしています。
拡大してみると、シクロプロピル基上の置換基を側鎖が取り囲んでいます。「大きい置換基は好まれない」というのは複合体構造でも納得できそうです。
また、親水性のArgがあるので、疎水性のメチル基よりも「分極した電子求引基の方が好まれる」といった考察も可能かもしれません。
・・・このままではよくわからないので、上の構造を静電ポテンシャル図で描画してみましょう!
2-3. ESP-DNNの結果で親和性を考察しよう
タンパク質(Tyk2)と上記3つのリガンド構造をESP-DNNで計算してみました。Google Colab上で計算し、NGL viewerで描画しています。具体的な計算と描画の方法は前回の記事をご参照ください。
2-3-1. タンパク質
まずタンパク質の静電ポテンシャル図はこんな感じです。
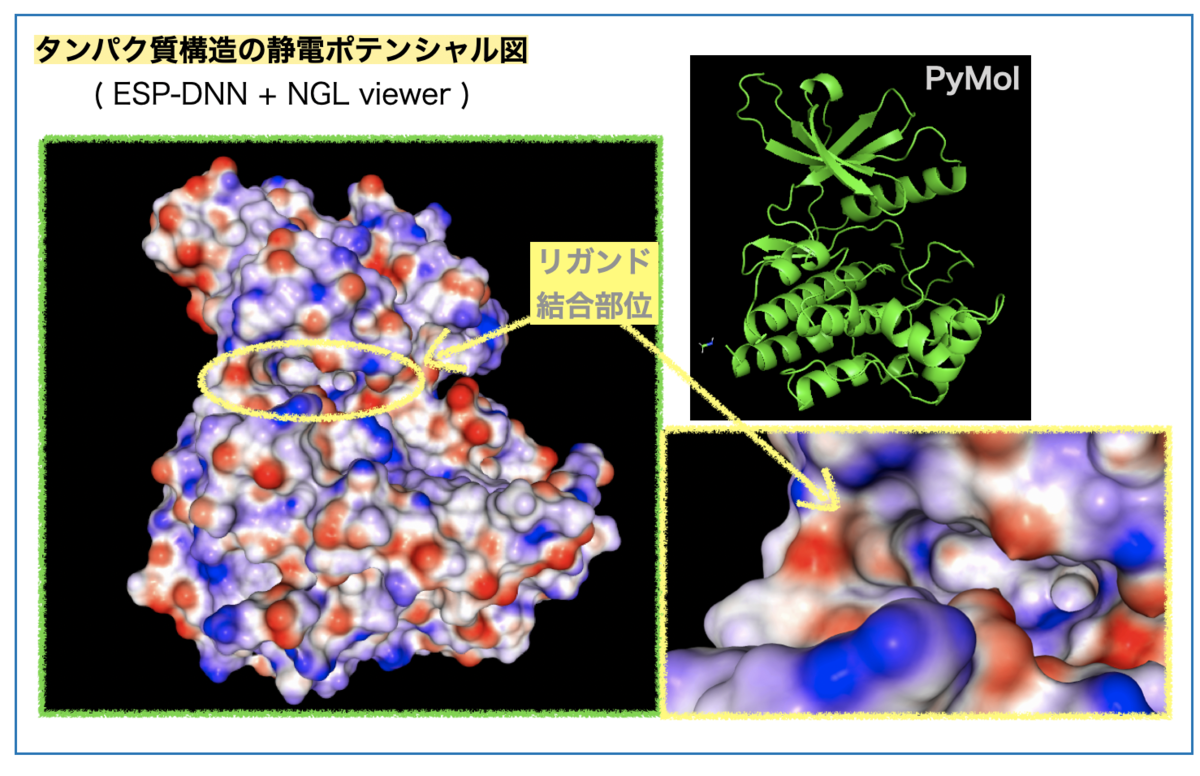
ESP図の赤い部分の原子は負の(部分)電荷をもち、青い部分の原子は正の(部分)電荷をもちます。
真ん中左寄りのくぼみがリガンドの結合するポケットです(黄色丸枠)。ポケットを拡大(右下)すると右奥が青色、溶媒に面した左部分に青と赤色が混在しています。
リガンドのシクロプロピル基周辺は溶媒に面した向かって左に相当します。この付近のESPの色がどの残基に対応するか?、眺めてみましょう。
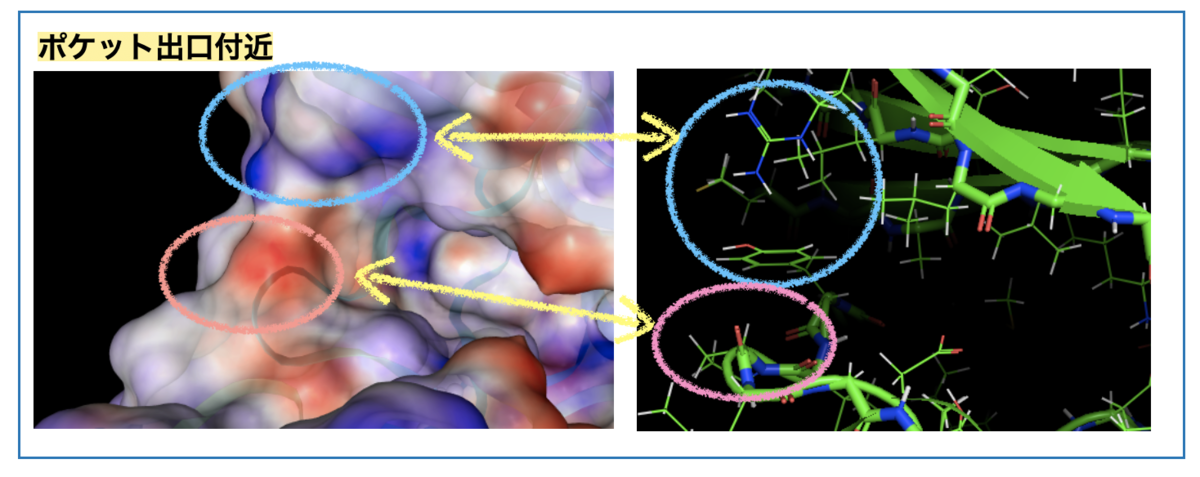
凡そですが、青い箇所は先に見たArgやTyrの側鎖に対応し、赤い箇所は主鎖(Pro)のカルボニル酸素に対応していそうです。*3
水素結合のドナーになりそうな水素原子近辺が青(+)、アクセプターになりそうな箇所が赤(-) と解釈することができるかもしれません。
2-3-2. リガンドの比較
つぎにリガンドのESP図を見てみましょう。こんな感じです。

リガンドの右側、ジクロロベンゼンをみるとCl基以外の水素原子が青色(+) になっています。ベンゼン環上で置換基導入が他の位置に及ぼす電子的な影響が視覚的でわかりやすいですね!
シクロプロピル基は左側、黄色の丸枠で囲んだ部分です。シクロプロピル基の置換基について以下の特徴が見えます。
- フッ素置換(
lig_jmc_23)ではFが赤色
- フッ素置換(
- 無置換(
lig_ejm_46)では青みがかった白
- 無置換(
- メチル置換(
lig_jmc_28)では青みがかった白の大きな構造
- メチル置換(
F以外ではシクロプロピル基全体がプラスっぽく、Fではマイナスっぽさが追加されている感じでしょうか?
置換基とは反対側の面からシクロプロピル基を眺めてみましょう。
こんな感じ。
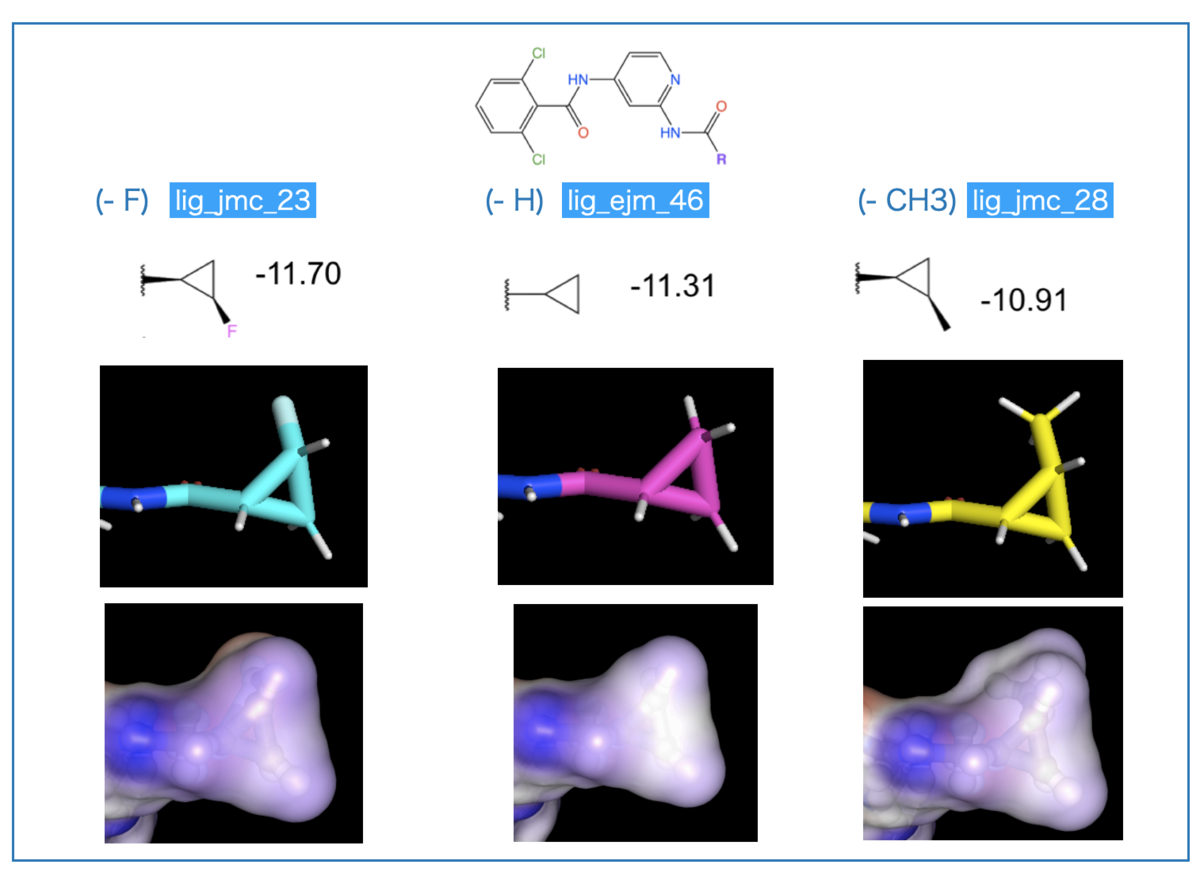
面白いことに、F置換は、無置換やメチル置換と比べて青色が濃くなっています。強い電子求引基で引っ張られた逆側にプラス性が強く現れるというのはわかりやすいですね!
2-3-3. リガンドとタンパク質の比較
タンパク質とリガンドをそれぞれ確認したので、組み合わせるとどうなるか?重ねてみましょう。
まずは一番シンプルな無置換の構造です。
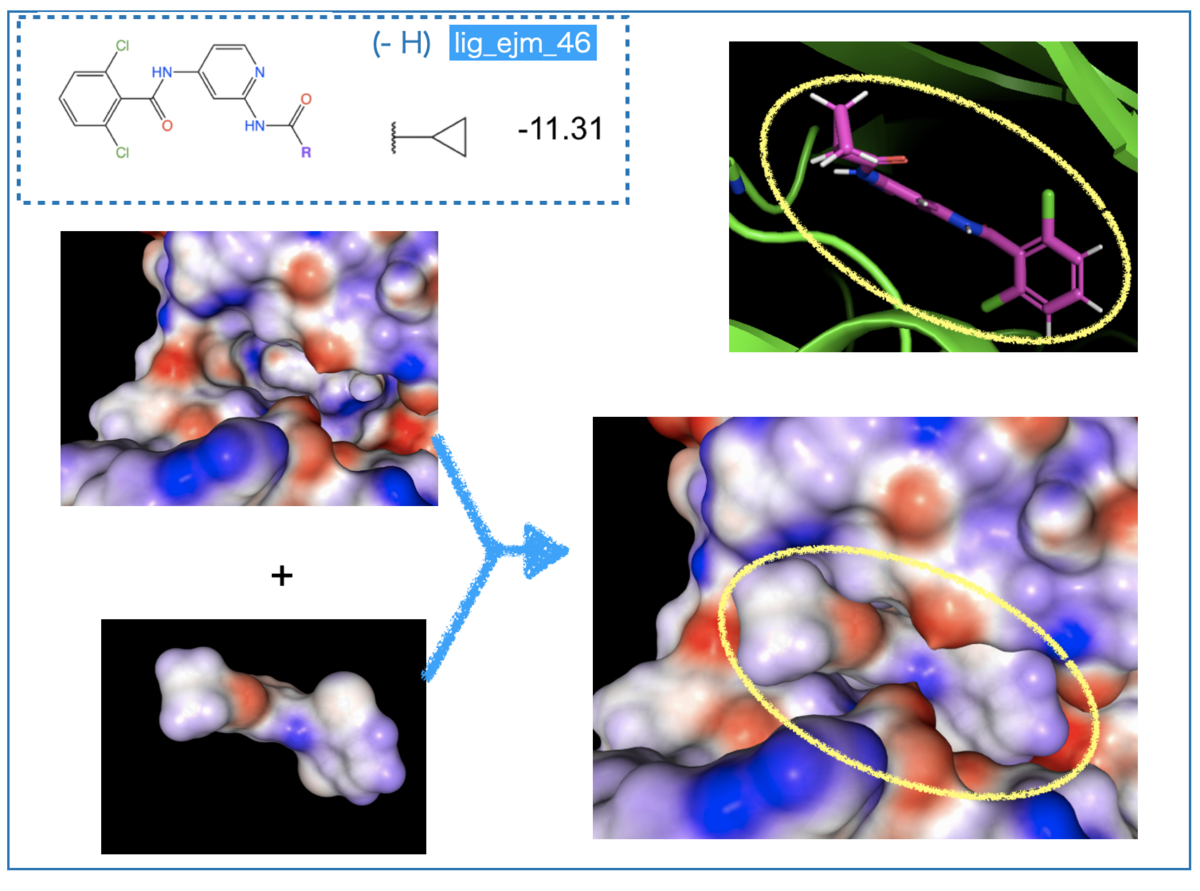
リガンド右側、ジクロロベンゼンの青い箇所がタンパク質側の赤い静電ポテンシャル面と接しているのが見えます。相補的な赤と青がタンパク-リガンドで接しており、相互作用に適していると考察できそうです。
また、リガンド中央の赤い箇所はシクロプロピル基に隣接したアミド結合のカルボニル酸素です。こちらもタンパク質側の青みがかった部分と接しており、相補的な組み合わせになっています。
データセットで「共通の骨格部分がタンパク質との相互作用に適した構造で一定の親和性を担保している」と考えると興味深いですね。
ついで活性の良いフッ素置換です。
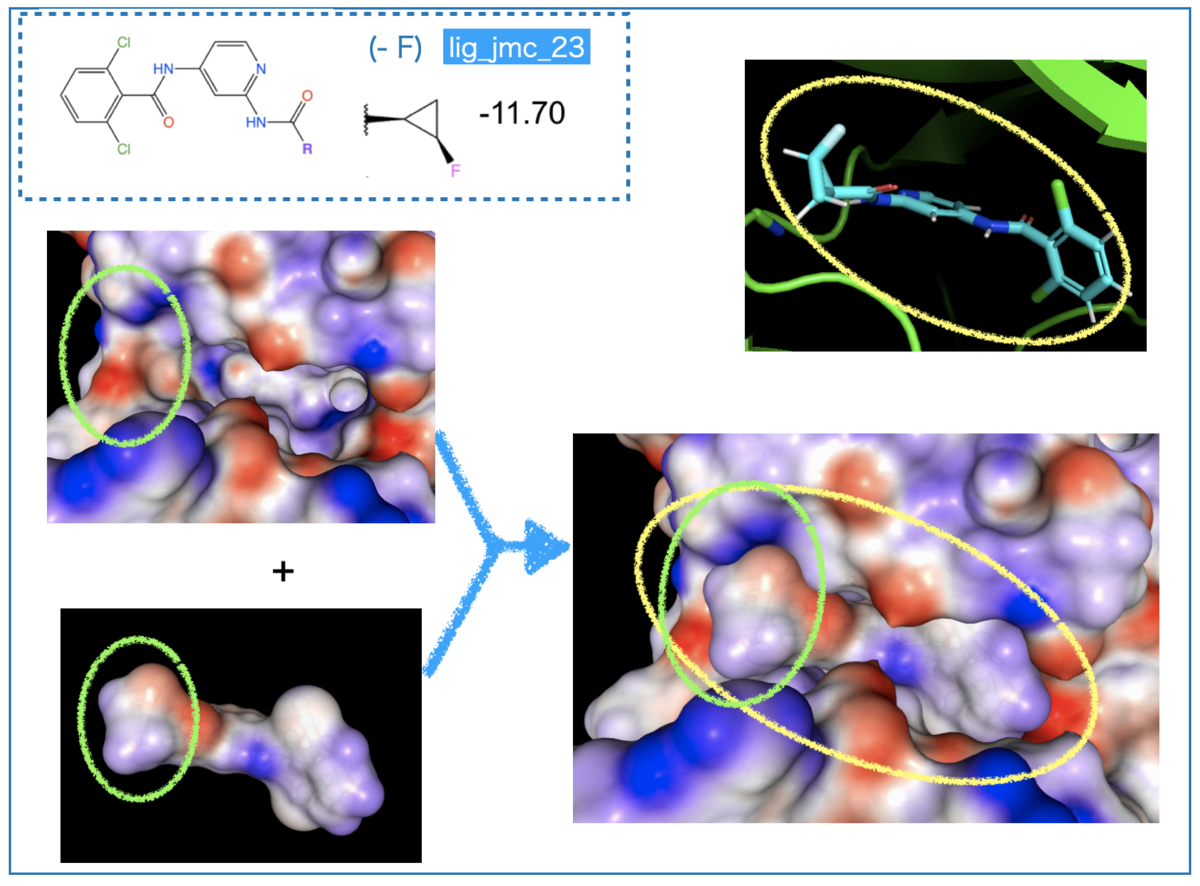
共通骨格は無置換と同じなので、シクロプロピル基(左側)に着目します。
F置換により赤色の箇所が増えています。ここと接するタンパク質の表面は青色となっています(先に見たArg側鎖 etc.の領域に相当)。
つまり、F置換で相補的な静電ポテンシャル面が増加しており、これによって親和性が向上したと考察できそうです。
またリガンド上で、F置換は置換基と反対側のシクロプロピル基表面をより濃い青色に変化させていました。タンパク質ポケットを見ると該当箇所は赤色となっています(上図左の緑丸)。
重ねた図では見えなくなっていますが、「赤色(タンパク)と濃い青色(リガンド)が接している」ため、この箇所でも相補性が良くなっていると推測されます。
次に、活性の落ちるメチル基置換です。
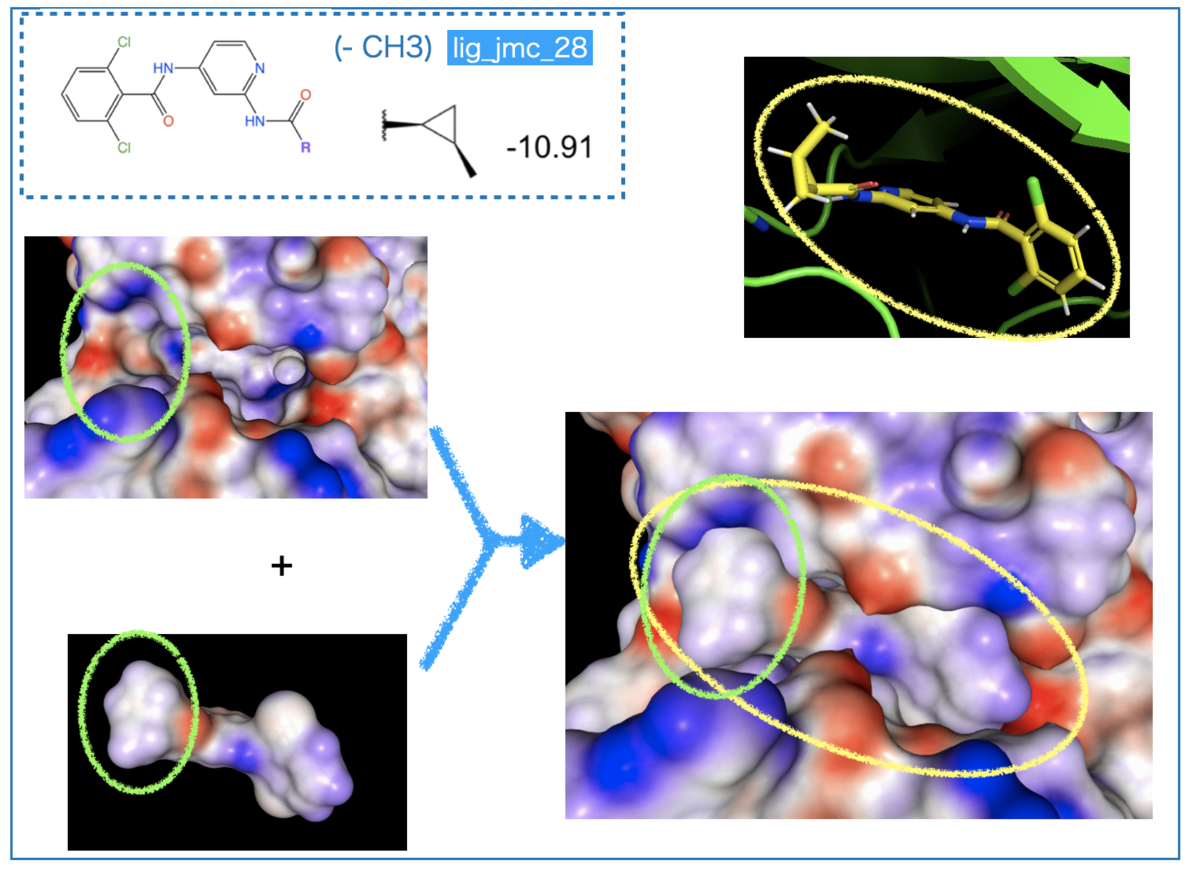
導入されたメチル基は静電ポテンシャルがほぼニュートラル(白〜薄い青色)です。複合体の左側、緑色の丸で囲んだ箇所を見ると、タンパク質の青色表面とメチル基の表面が接しています。
「(部分)電荷を帯びている箇所にニュートラルなものが当たっている」という状態で、相補性が良いとは言い難くなっています。
つまり、「置換基の導入によりタンパクとぶつかる面が増えたが、静電ポテンシャルの相性でメリットがないため、立体障害により親和性が落ちた」と考察できそうです。
「立体障害が親和性にネガティブに働きそう」というのは(2次元構造式の)構造活性相関やPyMolの描画で見た内容とも合いそうですね。
以上をまとめると、小さな置換基でタンパク質と相補的な静電ポテンシャル表面をつくることができる電子求引性のフッ素導入は親和性の向上に最適だった、と言えそうです。
3. おわりに
以上、今回はESP-DNNで計算した静電ポテンシャル図をもとに、Tyk2キナーゼ阻害剤の親和性の差について考察してみました。
定性的な議論ではありますが、「タンパク質とリガンドの表面の色が相補的(赤 - 青)となることと、親和性が良い(ΔG_expが小さい)」ことに関係性がありそうなことが見えました。
(2D/3Dの)構造式や複合体を普通に描画して眺めるだけではわからない観点(ESP)をとりいれることで、一歩踏み込んで活性について議論できそうなことがわかってよかったです。
ESPをまともに計算しようとすると量子力学計算が必要でどうして良いかわかりませんが、ESP-DNNを使うことで簡単かつ高速で計算ができました。
論文のタイトル通り、まさしく実用的(Practical)なツールですね。
Practical High-Quality Electrostatic Potential Surfaces for Drug Discovery Using a Graph-Convolutional Deep Neural Network J. Med. Chem. 2020, 63, 16, 8778–8790
すばらしいツールを公開してくださっている研究者の皆様に感謝です!
さあ、ESP-DNNで観察眼を鍛えて、創薬人格付けチェックに正解できる能力者(エスパー)に君もなろう!
おしまい。
(おまけ)ダジャレ師匠の素晴らしい記事
「私のキャリアパス紹介 〜アカデミアから民間企業に転職して」 小寺正明(Preferred Networks)
静電ポテンシャルからタンパク質-リガンド複合体を眺めよう 〜パート①:ESP-DNNの使い方〜
もはや元旦恒例となっている創薬ちゃん(@souyakuchan)さん主催の創薬人格付けチェック!
元旦恒例 #創薬人格付けチェック!
— 叢雲くすり (創薬ちゃん) (@souyakuchan) 2022年1月1日
今回はタンパク質側も実験構造と予測構造を混ぜてあり余計に訳分からなくした。画像(平行法ステレオ図) に示す4つの結合様式のうち、1つが概ね正しい複合体構造だ。
正しいと思うのは何番だろうか? 次のツイートで投票を取る。#souyakuchan_quiz#格付けチェック pic.twitter.com/9SL7bd1sBN
皆さんもちろん正解してますよね?・・・私は毎年外しています(解説を読んでもよくわからない)。
ぶっちゃけリガンドとタンパク質の複合体の図を見ても「当てはまりが良い!」とか、「ここが変!」とかさっぱりわかりません。
「観察眼を鍛えたい!もう一歩踏み込んだ視点が欲しい!」ということで、今回は静電ポテンシャル図(ESP)を描いて複合体を眺めてみたいと思います。
利用するツールは①ESP-DNNで、計算対象としては②TYK2キナーゼ阻害剤データセットを用います。
この記事ではまず簡単な分子(1置換ベンゼン)を例にESP-DNNの使い方を把握します(複合体の描画は次回)。*1

1. ESP-DNN
1-1. ESPの復習
静電ポテンシャル(Electrostatic Potential, ESP)は「ある分子の周りに+1価の電荷をおいた際に、その電荷が感じるポテンシャルエネルギー」です。
これを分子について可視化するために分子表面として描いたのが静電ポテンシャル図(Electrostatic Potensial Surface)です。等電子密度面に静電ポテンシャル(電位)を色で表現したもので、分子の静電的な特徴を簡単に把握できます。
学部の有機化学で1置換ベンゼンの反応性(ortho-, meta-, para- 配向性)の説明で出てきたりするやつですね。
こういうの。

赤い部分の原子は負の(部分)電荷をもち、青い部分の原子は正の(部分)電荷をもちます。置換基による芳香環上の変化が目に見えるのが面白いですね。*2
ところで以前、どこかで「ニトロベンゼンとピリジンはESPを描くとめっちゃ似てる!」って力説してる先生がいらっしゃった気がします。確かに似てるかも・・・
ってなわけで(?)、ESPをつかって可視化すると構造式で単純に描く以上に分子の性質を考察することができます。生理活性物質への応用を考えると、「リガンドとタンパク質の静電的な相補性の観点から、親和性・活性について議論できる!」ってなりそうです。
つまり、ESP力を鍛えれば相互作用の観察力が上がって創薬人格付けチェックに正解できるはず!
・・・知らんけど
1-2. ESP-DNNって?
さて、とても魅力的なESPによる可視化ですが、きちんと計算しようとすると量子力学(QM)が必要です。例えば「化学の新しいカタチ」さんは以下の記事でPsi4を使った計算方法を解説してくださっています。
・・・QM計算しんどいですね。
「面倒な計算はディープラーニングで置き換えよう!」ということで、QMのデータセットを学習して短時間の計算で置き換えられるようにしたのがESP-DNNです。
Practical High-Quality Electrostatic Potential Surfaces for Drug Discovery Using a Graph-Convolutional Deep Neural Network
Prakash Chandra Rathi, R. Frederick Ludlow, and Marcel L. Verdonk
J. Med. Chem. 2020, 63, 16, 8778–8790 (Open Access)
Astex Pharmaceuticalsの研究者によって開発されたプログラムで、GitHubで公開してくださっています。(Apache-2.0ライセンス)
また、ESP-DNNについては@iwatobipen先生が以下の記事で取り上げてくださっています。
Electrostatic Potential Surface(ESP) calculation with GCNN #RDKit #chemoinformaticsiwatobipen.wordpress.com
上記GitHubでは、Python 2系のコードで書かれていたESP-DNNをPython3系にアップデートしたものを公開してくださっています。
これは遊ぶしかないですね!
・・・でも残念ながら私のMacではうまく動きませんでした。
2. ESP-DNNをGoogle Colabで
OSが合ってないならGoogle Colabを使えばいいじゃない!ということでちょっとだけ書き換えました。
conda createで環境構築できるようにenvironment.ymlをPython3(@iwatobipen先生の記事で公開されている設定)に合わせただけです。
Google Colab上で以下を実行すればESP-DNNを使うためのconda環境(esp-dnn-env)ができます。
# Linux用のMinicondaの環境を作成 !wget -c https://repo.continuum.io/miniconda/Miniconda3-latest-Linux-x86_64.sh !chmod +x Miniconda3-latest-Linux-x86_64.sh !bash ./Miniconda3-latest-Linux-x86_64.sh -b -f -p /usr/local # GitHubからESP-DNNをもってくる !git clone https://github.com/magattaca/ESP_DNN.git # 作業ディレクトリを移動 %cd ESP_DNN # condaの仮想環境をyamlから作成 !conda env create -f ESP_DNN/environment.yml
これで計算環境の準備はおしまいです(すこし時間かかります)。
ESP-DNNをつかって静電ポテンシャルを計算するコマンドは、計算対象が「リガンドか?タンパク質か?」によって少し変わります。
いずれにせよ入力はPDBファイルなので適当に準備してください(RDKitならChem.MolToPDBFileです)。
リガンド(低分子)の場合は、以下のコマンドで「①仮想環境をアクティベートして、②ligand_filesディレクトリにある複数のPDBファイルをまとめて計算」できます。
%%bash source activate esp-dnn-env python -m esp_dnn.predict -m ligand -i ligand_files
タンパク質の場合は引数-m(計算モード, mode)をproteinにすればOKです。
%%bash source activate esp-dnn-env python -m esp_dnn.predict -m protein -i protein_files
上記でprotein_filesディレクトリにあるPDBファイルが計算されます(ディレクトリ名は適宜修正してください)。
計算結果はpqr形式のファイルで、入力のPDBファイル名のあとに.pqrが追加されたファイルが同じディレクトリ内に作成されます。
これで計算したものが先の1置換ベンゼンです。簡単ですね!
3. NGL viewerで可視化
ESP-DNNの計算結果の描画はNGL viewerがオススメされています。
- NGL viewer : http://nglviewer.org/ngl/
上記のURLにアクセスして「File → open」で目的の「.pqrファイル」を選びます。もしくはファイルをドラッグ&ドロップでもOKです。
例えばニトロベンゼンのpqrファイルだとこんな感じ。

PDBファイルを基にしているので結合次数の情報が入っていない(ベンゼンが全て単結合)であることにご注意ください。
ESP図を表示する手順は「① 表面(Surface)描画を追加して、② 描画方法を静電ポテンシャルに変更」です。
まず表面描画を追加します。
- 右枠上の横三本線マークをクリックして
Structure オプションのメニューを開く
- 右枠上の横三本線マークをクリックして
Representationにsurfaceを追加
- 分子表面が描画され右枠に
surfaceメニューがあらわれる
- 分子表面が描画され右枠に

ついで描画方法を静電ポテンシャルに変更します。
surfaceメニューの横三本線マークをクリックしてRepresentation オプションのメニューを開く
- 各項目を変更
-
surface typeでavを選択 -
scale factorを4.0に変更 -
radius Typeをexplicitに変更 -
opacityをスライドバー調整(表面が透けて骨格が見える) -
colorSchemeをelectrostaticに変更 -
colorScaleをRed-White-Blueに変更
-
- 各項目を変更

以上の設定で以下の図ができます。

「目のアイコン」をクリックすると描画の表示をON/OFFできるので、複数の分子を1つのViewerで見るときに便利です。
4. 拡張子PQRと謎の原子
4-1. PQR?
さて、さらっと流しましたがPQRファイルとはなんでしょうか?
PQRはPDBをベースにしたフォーマットで、「PはPDB、Qは電荷(charge)、Rは半径(radius)」を意味するそうです。
この意味に合わせて、保持する情報が以下のように変更されています。*3
- ①
PDB: 占有率(occupancy)→PQR: 原子の電荷 (atomic charge, Q) - ②
PDB:温度因子(B factor) →PQR:原子半径(atomic radius, R)
但し、カラム(列)の位置はPQRとPDBでズレていることも多いそうです。
先のニトロベンゼンのファイルで比較してみましょう。
こんな感じ

各行の座標(xyz)情報は同じですが、それ以降の数字が変わっていますね。
4-2. 謎の原子?
ところで上図の4行とも炭素原子(C)ですが、面白いことにPQRファイルの原子半径は「C1, C2, C3 → 1.700」と「C4 → 1.780」で異なっています(黄色枠で示した箇所) 。
このC4はニトロ基置換のイプソ位になります。もう一度描画を確認すると、炭素原子のうちC4だけ白い球が追加されています。他の炭素との違いを反映して原子半径も異なっているのかもしれません(???)

この白い球の原子名はHpとなっていて、ニトロ基の窒素原子(N)、酸素原子(O)上にも同様にHpという名前の球が追加されています。また、酸素原子上には他にもHlpという原子が追加されています。
Hとついていますが水素原子ではなさそうです。追加の様子を見る限り非共有電子対や(芳香族以外の)二重結合の電子を表すダミーのようにも見えますが、PQRフォーマットやESP-DNNの説明をみてもそれらしい記述がありませんでした。
お分かりの方、ご教示いただけると嬉しいです。*4
5. おわりに
以上、今回はタンパク質-リガンド複合体を眺めるための観察方法「静電ポテンシャル図」を試す準備として、簡易計算ツール ESP-DNN の使い方と描画方法を確認しました。
ESPの計算には量子力学が必要で大変そうですが、ディープラーニングで置き換えたESP-DNNを使えばとても簡単に計算できました。素晴らしいツールを公開してくださっている皆様に感謝です。
結果の確からしさ(量子力学計算との比較)は検証できませんでしたが、そもそも私はQM計算できない・・・。できない人向けの簡易ツールということで許してください。
次回、実際にリガンドやタンパク質を計算してみたいと思います。
間違いが多いと思うのでご指摘いただけると嬉しいです。ではでは!
*2:静電ポテンシャルの説明と見方についてははこちらの記事「静電ポテンシャルマップの誤解」を参考にさせていただきました。ずっと誤解してた。。。
*3:参考:Jmol/JSmol wiki File formats/Coordinates: PQRより
*4:なお、ESP-DNNのexamplesにあるPQRファイルにも同様にHpやHlpがあるので計算が失敗しているわけではなさそうです。
RDKitで3次元構造に水素原子を付加するときの設定(addCoords)
RDKitの基本的な操作についてのメモです。
「Chem.AddHs()の引数のaddCoords=Trueを今更知った!」って話です。
よくやるミス
立体構造の座標が入ったMolファイル、SDFファイルから化合物を読み込んだ後で、「水素原子を付け足したいなー」って時があります。
まず、molファイルからmolオブジェクトを作ります。
from rdkit import Chem from rdkit.Chem.Draw import IPythonConsole m = Chem.MolFromMolFile('test.mol') IPythonConsole.drawMol3D(m)

で、何も考えずにChem.AddHs()とやって、こんな構造がでてがっかりします。
mH = Chem.AddHs(m) IPythonConsole.drawMol3D(mH)

遠近法みたいですね。
addCoords=Trueをつけると?
違う、そうじゃない!ということでaddCoords=Trueします。
true_mH = Chem.AddHs(m, addCoords=True)
IPythonConsole.drawMol3D(true_mH)

そう、これが欲しかった!
何が起きてる?
何が起きてるのか座標を確認してみましょう。
addCoords=Trueを設定しなかった場合のMOLブロックはこんな感じです。
print(Chem.MolToMolBlock(mH)) """ EFZ RDKit 3D 30 32 0 0 1 0 0 0 0 0999 V2000 -4.6650 -32.8110 24.1290 Cl 0 0 0 0 0 0 0 0 0 0 0 0 0.7540 -37.4060 23.9780 F 0 0 0 0 0 0 0 0 0 0 0 0 -1.2240 -36.9050 24.5760 F 0 0 0 0 0 0 0 0 0 0 0 0 -0.8430 -37.4960 22.5660 F 0 0 0 0 0 0 0 0 0 0 0 0 1.5560 -35.7230 20.0590 O 0 0 0 0 0 0 0 0 0 0 0 0 0.9480 -35.2860 22.1560 O 0 0 0 0 0 0 0 0 0 0 0 0 -0.6250 -35.1620 20.4090 N 0 0 0 0 0 0 0 0 0 0 0 0 -1.6090 -34.5740 21.2770 C 0 0 0 0 0 0 0 0 0 0 0 0 -2.8080 -34.0130 20.7730 C 0 0 0 0 0 0 0 0 0 0 0 0 -3.7390 -33.4660 21.6780 C 0 0 0 0 0 0 0 0 0 0 0 0 -3.4980 -33.4840 23.0470 C 0 0 0 0 0 0 0 0 0 0 0 0 -2.3320 -34.0240 23.5560 C 0 0 0 0 0 0 0 0 0 0 0 0 -1.4060 -34.6050 22.6750 C 0 0 0 0 0 0 0 0 0 0 0 0 -0.0960 -35.2860 23.1970 C 0 0 0 0 0 0 0 0 0 0 0 0 0.4550 -34.6070 24.3910 C 0 0 0 0 0 0 0 0 0 0 0 0 0.8900 -34.0500 25.3200 C 0 0 0 0 0 0 0 0 0 0 0 0 1.5190 -33.2180 26.6670 C 0 0 0 0 0 0 0 0 0 0 0 0 2.2540 -32.3400 26.2030 C 0 0 0 0 0 0 0 0 0 0 0 0 1.0630 -32.0720 26.5920 C 0 0 0 0 0 0 0 0 0 0 0 0 -0.3570 -36.7960 23.5830 C 0 0 0 0 0 0 0 0 0 0 0 0 0.6810 -35.4120 20.8040 C 0 0 0 0 0 0 0 0 0 0 0 0 0.0000 0.0000 0.0000 H 0 0 0 0 0 0 0 0 0 0 0 0 0.0000 0.0000 0.0000 H 0 0 0 0 0 0 0 0 0 0 0 0 0.0000 0.0000 0.0000 H 0 0 0 0 0 0 0 0 0 0 0 0 0.0000 0.0000 0.0000 H 0 0 0 0 0 0 0 0 0 0 0 0 0.0000 0.0000 0.0000 H 0 0 0 0 0 0 0 0 0 0 0 0 0.0000 0.0000 0.0000 H 0 0 0 0 0 0 0 0 0 0 0 0 0.0000 0.0000 0.0000 H 0 0 0 0 0 0 0 0 0 0 0 0 0.0000 0.0000 0.0000 H 0 0 0 0 0 0 0 0 0 0 0 0 0.0000 0.0000 0.0000 H 0 0 0 0 0 0 0 0 0 0 0 0 1 11 1 0 2 20 1 0 3 20 1 0 4 20 1 0 5 21 2 0 6 14 1 0 6 21 1 0 7 8 1 0 7 21 1 0 8 9 2 0 8 13 1 0 9 10 1 0 10 11 2 0 11 12 1 0 12 13 2 0 13 14 1 0 14 15 1 0 14 20 1 0 15 16 3 0 16 17 1 0 17 18 1 0 17 19 1 0 18 19 1 0 7 22 1 0 9 23 1 0 10 24 1 0 12 25 1 0 17 26 1 0 18 27 1 0 18 28 1 0 19 29 1 0 19 30 1 0 M END """
水素原子(H)の座標にご注目ください。複数ある水素原子のXYZ座標が全て「0.0000」になっています。
Chem.addHs()はデフォルトでは水素原子の座標を原点にするようです。付加した水素原子がすべて原点に集まっているので、3D描画では原点から飛び出る結合が描かれていたみたいです。
addCoords=TrueのMOLブロックはこうなっています。
print(Chem.MolToMolBlock(true_mH)) """ EFZ RDKit 3D 30 32 0 0 1 0 0 0 0 0999 V2000 -4.6650 -32.8110 24.1290 Cl 0 0 0 0 0 0 0 0 0 0 0 0 0.7540 -37.4060 23.9780 F 0 0 0 0 0 0 0 0 0 0 0 0 -1.2240 -36.9050 24.5760 F 0 0 0 0 0 0 0 0 0 0 0 0 -0.8430 -37.4960 22.5660 F 0 0 0 0 0 0 0 0 0 0 0 0 1.5560 -35.7230 20.0590 O 0 0 0 0 0 0 0 0 0 0 0 0 0.9480 -35.2860 22.1560 O 0 0 0 0 0 0 0 0 0 0 0 0 -0.6250 -35.1620 20.4090 N 0 0 0 0 0 0 0 0 0 0 0 0 -1.6090 -34.5740 21.2770 C 0 0 0 0 0 0 0 0 0 0 0 0 -2.8080 -34.0130 20.7730 C 0 0 0 0 0 0 0 0 0 0 0 0 -3.7390 -33.4660 21.6780 C 0 0 0 0 0 0 0 0 0 0 0 0 -3.4980 -33.4840 23.0470 C 0 0 0 0 0 0 0 0 0 0 0 0 -2.3320 -34.0240 23.5560 C 0 0 0 0 0 0 0 0 0 0 0 0 -1.4060 -34.6050 22.6750 C 0 0 0 0 0 0 0 0 0 0 0 0 -0.0960 -35.2860 23.1970 C 0 0 0 0 0 0 0 0 0 0 0 0 0.4550 -34.6070 24.3910 C 0 0 0 0 0 0 0 0 0 0 0 0 0.8900 -34.0500 25.3200 C 0 0 0 0 0 0 0 0 0 0 0 0 1.5190 -33.2180 26.6670 C 0 0 0 0 0 0 0 0 0 0 0 0 2.2540 -32.3400 26.2030 C 0 0 0 0 0 0 0 0 0 0 0 0 1.0630 -32.0720 26.5920 C 0 0 0 0 0 0 0 0 0 0 0 0 -0.3570 -36.7960 23.5830 C 0 0 0 0 0 0 0 0 0 0 0 0 0.6810 -35.4120 20.8040 C 0 0 0 0 0 0 0 0 0 0 0 0 -0.9030 -35.4093 19.4485 H 0 0 0 0 0 0 0 0 0 0 0 0 -3.0092 -34.0045 19.6916 H 0 0 0 0 0 0 0 0 0 0 0 0 -4.6687 -33.0188 21.2963 H 0 0 0 0 0 0 0 0 0 0 0 0 -2.1321 -33.9989 24.6374 H 0 0 0 0 0 0 0 0 0 0 0 0 1.6124 -33.9674 27.4668 H 0 0 0 0 0 0 0 0 0 0 0 0 3.1187 -31.9803 26.7800 H 0 0 0 0 0 0 0 0 0 0 0 0 2.8248 -32.2051 25.2724 H 0 0 0 0 0 0 0 0 0 0 0 0 0.2807 -31.8348 25.8560 H 0 0 0 0 0 0 0 0 0 0 0 0 0.6089 -31.3601 27.2970 H 0 0 0 0 0 0 0 0 0 0 0 0 1 11 1 0 2 20 1 0 3 20 1 0 4 20 1 0 5 21 2 0 6 14 1 0 6 21 1 0 7 8 1 0 7 21 1 0 8 9 2 0 8 13 1 0 9 10 1 0 10 11 2 0 11 12 1 0 12 13 2 0 13 14 1 0 14 15 1 0 14 20 1 0 15 16 3 0 16 17 1 0 17 18 1 0 17 19 1 0 18 19 1 0 7 22 1 0 9 23 1 0 10 24 1 0 12 25 1 0 17 26 1 0 18 27 1 0 18 28 1 0 19 29 1 0 19 30 1 0 M END """
水素原子のXYZ座標に数値がはいっていました。
以上です。
おわりに
3次元構造に水素原子を付け足すときに、以下の記事に紹介してくださっているような方法をとったりしていました。
「①一度SMILESに戻して、②molオブジェクトを作り直し、③水素原子を付加して、④3次元座標を生成」といった手順です。
これだと元のファイルの折角の3次元座標を捨ててしまっていて、もったいないなーと思っていました。簡単な設定で解決できることがわかってよかったです。
・・・むしろなぜ今まで気づかなかったのか。
ところで今回例につかった化合物はエファビレンツです。
この不斉をどう合成するか??・・・答えはアートオブプロセスケミストリーで!
おしまい。
OpenMMをステップバイステップで 〜Part 10 全体のまとめと感想、あと失敗例〜
OpenMMの使い方を順番にたどるシリーズのまとめです。
この記事はシリーズ全体の総括と各記事へのリンクまとめが主目的です。
また、備忘録としてうまくできなかったことものせておきます。ProLIFの踏み込んだ設定やParmEdのファイル変換機能にふれています。
1. 全体の総括
「OpenMMをステップバイステップで」というタイトルでMDシミュレーションの計算の設定や実行、結果の解析方法について複数の記事にまたがって眺めてきました。
前回で「タンパク質ー低分子複合体のシミュレーション解析」まで確認し、(Part 1で設定した)当初の目標 「TeachOpenCADDのT019 · Molecular dynamics simulationとT020 · Analyzing molecular dynamics simulations の内容」を全てたどり終わりました。区切りが良いのでこのシリーズは一度終わりとして、全体の総括をしたいと思います。
各記事でとりあげた内容とツールを以下の表にまとめています。最初からタンパク質-低分子複合体のシミュレーションを行うのはハードルが高かったので、タンパク質単独の前処理方法から始めて、順番に計算の設定・実行、解析を眺めました。
| 記事リンク | おもな内容 | ツール |
|---|---|---|
| Part 1 | GUIツールを使ったタンパク質構造の前処理 | OpenMM Setup |
| Part 2 | Part 1の前処理操作をPythonで実行 | PDBFixer |
| Part 3 | GUIツールを使ったシミュレーション条件の設定 | OpenMM Setup |
| Part 4 | Google Colab上でMDシミュレーションを実行 | OpenMM |
| Part 5 | シミュレーション実行スクリプトの仕組みと書き方(Python) | OpenMM |
| Part 6 | トラジェクトリ解析① (RMSD,RMSF,回転半径) | MDAnalysis, NGLView |
| Part 7 | トラジェクトリ解析② (PCA, cross correlation) | MDAnalysis, pytraj |
| Part 8 | 低分子-タンパク質複合体の計算系の設定と計算 | OpenMM, OpenFF, MDTraj |
| Part 9 | 低分子-タンパク質複合体のトラジェクトリ解析 | ProLIF, MDAnalysis |
メインに利用したツールはOpenMMでしたが、他にも様々なオープンソースのツールが必要でした。出てくるツール群の概要はだいたい以下の記事にまとめてあります。
また、追加の情報として「OpenMMのよくある質問(FAQ @ Github)」を以下に翻訳しました。MD計算の設定や結果について書かれていて参考になりました。
2. きっかけと感想
さて、今回MDシミュレーションを試してみようと思ったのは言うまでもなくTeachOpenCADDという素晴らしい教材が用意されていたからですが、それに加えてTwitterでMaking it rainというプロジェクトを教えていただいたことも大きかったです。
Making it rainについてはこちらの記事で取り上げました。
MD計算にあこがれはあったものの、難しそうだし高性能なコンピュータがないとどうしようもないと思っていましたが、Google Colabを利用して計算できること、使いやすいオープンソースのプログラムが色々と開発されていると知って「これは遊べるぞ!!」となりました。
OpenMMにGUIツール(OpenMM Setup)が提供されていることを知ったのも大きかったです。「① GUIで使い方の流れと出力を把握 → ② Pythonのコードで同じことができるか確認」という手順を踏めたことで、私でも凡その流れを把握することができました。
実際に計算・解析してみて、「おおっ本当にタンパク動くんだな!」「X線だと綺麗にはまっているリガンドもMDだと割とパタパタ動くんだな!」となって楽しかったです。
特に、複合体のMDトラジェクトリで元の複合体構造にはなかった水素結合がリガンドとタンパクの間に形成されていたのは驚きでした。「相互作用も動的なもので、共結晶構造だけが唯一の正解の結合ポーズではないんだなー。」ってことが実感できたのが何よりでした。
さて、優秀な先人の皆様のおかげで学習する環境は整っているものの、私にとっては難しく、予想以上に長期のシリーズ記事になってしまいました。ここまでお付き合いいただきありがとうございました。
取り上げている計算内容はTeachOpenCADDとほとんど一緒なのに長さは約5倍!!・・・この無駄な長さの中に少しでも役立つ情報があればとても嬉しいです。
3. このシリーズでできなかったこと
MD計算は非常に範囲が広く、深い分野なのでこのシリーズで扱えなかった内容はとてもたくさんあります。
例えば、タンパク質の構造前処理一つとっても@Ag_smith先生のこちらの記事ほどは踏み込めていません。
ジスルフィド結合や金属イオンなど、難しいポイントはたくさんありそうです。
また、低分子の力場についてもOpen Forcefieldで開発されている新しい力場をうまく適用することができませんでした。
低分子-リガンド複合体のシミュレーションということで、「相互作用のエネルギーはどうなるのか?」「結合親和性の見積もりにはどのように活かせば良いのか?」といった点も非常に興味深いところではありますが、私の能力では手に負えず扱うことができませんでした。
AmberではMMPB-SA法(?)といったツールがあるようです。(以下の記事ではシミュレーション時間 500nsくらいは欲しい、といった記載がありました。Google ColabのGPUでも1nsに1時間くらいかかったのに・・・)
OpenMMを使った結合自由エネルギー計算ツールとしてはChodera Labの開発したYANKといったものがあるようです。
まだまだ他にもトピックがたくさんありますね!もっといい方法があるよー、などなどご教示いただけると嬉しいです。
4. (おまけ)試したけどうまくいかなかったもの
総括は以上として、以下にはうまくいかなかった操作を備忘録として置いておきます。
4-2. ProLIFの相互作用パラメータを変えた再解析
4-2-1. 課題
記事(Part 9)では「低分子 - タンパク質複合体」のMDシミュレーションのトラジェクトリ解析で水素結合の解析を行いました。その中で、ProLIFとMDAnalysisに水素結合検出の差がありました。この点についてProLIFの相互作用の定義を変更することで解析結果が変わるか検討しました。
4-2-2. おさらい
まずおさらいですが計算対象の構造はPDB ID: 3POZでEGFRタンパクのキナーゼドメインとリガンド TAK-285のX線共結晶構造です。

図の通り共結晶構造からはEGFRのヒンジ領域「Met793の主鎖NH」と「リガンドのN原子」との間に水素結合ができても良さそうです。
実際、MDAnalysisによるトラジェクトリ解析では、デフォルトの定義「ドナー(D) - アクセプター(A) 距離 < 3.0Å」、「D - H - A角度 > 150°」を満たすフレームがいくつか見つかりました。

一方で、ProLIF を用いたInteraction Fingerprint解析(IFP)では、この領域に水素結合は検出されませんでした。
以上の原因を探るためProLIFの相互作用検出の定義を確認し、期待した相互作用を検出できるように定義を変更できるか検証します。
4-2-3. ProLIFの相互作用の定義
まず、ProLIFの相互作用の定義について、元論文の記述を確認しましょう。
- 論文:Bouysset, C., Fiorucci, S. ProLIF: a library to encode molecular interactions as fingerprints. J Cheminform 13, 72 (2021). (オープンアクセス、CC BY 4.0)
判定基準の距離と角度はTable 2に書かれています。

図中に枠で示した通り、水素結合(HBAcceptor、HBDonor)は「距離 ≦ 3.5 Å、角度 130° 〜 180°」です。MDAnalysisの定義よりも緩いですね。こちらは問題なさそうです。
それでは判定基準の原子パターンはどうでしょうか?こちらはSMARTSパターンで定義されているようです。

HBAcceptorは「(N or O or F or アニオン)and (カチオンではない)」です(多分)。「中性か負電荷を帯びているN原子、O原子、F原子」と考えると水素結合のアクセプターとして納得です。
一方でHBDonorは原子番号を使って定義をされていて「窒素(#7)-H or 酸素(#8)-H or 硫黄(#16)-H」です。硫黄が入っているところに生体分子をターゲットとしたツールであることを感じますね。
ここで注目したいのはHBAcceptorの原子の種類の指定方法です。「N」のように大文字のアルファベットで書いた場合、SMARTSでは「アリファティックな窒素原子」を意味するはずです*1。ですので、芳香属性の窒素原子はこのアクセプターの定義では検出できない可能性があります。
4-2-4. RDKitでSMARTSパターンの認識をチェック
ProLIFの定義をふまえて「芳香族性の原子が水素結合アクセプターからはじかれている」可能性が出てきました。
「SMARTSパターンでどのような構造が認識されるか?」、RDKitで検証してみましょう。ProLIFも構造式の取り扱いはRDKitをベースとしているようなので、RDKitで検証しておけば挙動が予測できるはず・・・多分。
今回計算対象のリガンド(TAK-285)の構造を作って、HBAcceptorのSMARTSパターンと部分構造検索でマッチするか検証します。
from rdkit import Chem from rdkit.Chem import Draw # SMILESからTAK-285を構築 smi_tak285 = "CC(C)(CC(=O)NCCn1ccc2c1c(ncn2)Nc3ccc(c(c3)Cl)Oc4cccc(c4)C(F)(F)F)O" rd_tak285 = Chem.MolFromSmiles(smi_tak285) rd_tak285H = Chem.AddHs(rd_tak285) Draw.MolToImage(rd_tak285H)

SMARTSからMolオブジェクトを作ってGetSubstructMatchesでマッチする部分構造を見つけ、ハイライトして描画します。
# SMARTSのMolオブジェクト化 HBA_query = Chem.MolFromSmarts('[N,O,F,-{1-};!+{1-}]') # 部分構造検索と該当箇所の取り出し HBA_tak285 = rd_tak285H.GetSubstructMatches(HBA_query) matched_HBA = [a[0] for a in HBA_tak285] # 描画 Draw.MolToImage(rd_tak285H, highlightAtoms = matched_HBA)

少し小さいですが赤い丸で示されているのがSMARTSに適合した部分です。構造式の左から時計回りにOH基、アミド、アニリンN、エーテルのO、CF3基のFと言ったものが認識されています。
ここで芳香族ヘテロ環(ピロロピリミジン環?)の窒素原子はクエリにかかっていないことに注目です。
MDAnalysisで解析した対象のリガンド窒素原子は、ProLIFではそもそも水素結合アクセプターを取りうる原子として認識されていなかった可能性が示唆されました。
ちなみに、HBDonorの定義のように原子番号でSMARTSを定義するとどうなるでしょうか?
# N → #7に変更して再検証 # SMARTSのMolオブジェクト化 HBA_query_2 = Chem.MolFromSmarts('[#7,O,F,-{1-};!+{1-}]') # 部分構造検索と該当箇所の取り出し HBA_tak285_2 = rd_tak285H.GetSubstructMatches(HBA_query_2) matched_HBA_2 = [a[0] for a in HBA_tak285_2] # 描画 Draw.MolToImage(rd_tak285H, highlightAtoms = matched_HBA_2)

今度はリガンドの全ての窒素原子がハイライトされました。水素結合ドナーになりそうにない窒素原子(ピロール様のN?)まで含んでしまっているところが問題ではありますが、、、適切なクエリを作るのは難しいですね。
4-2-5. ProLIFの相互作用パラメーターを変えよう
RDKitによる検証で水素結合ドナーの定義を変えてやれば、前回の宿題の水素結合も認識される可能性が出てきました。
ProLIFでは検出する相互作用のパラメーターを変えたり、新しい相互作用を定義することができます。
ProLIFのデフォルトの各相互作用のクラスはドキュメントのprolif.interactionsに記載があり、水素結合アクセプターは「prolif.interactions.HBAcceptor(donor='[#7,#8,#16][H]', acceptor='[N,O,F,-{1-};!+{1-}]', distance=3.5, angles=(130, 180))」となっています。
アクセプターのパラメーターを変えた新しいクラス(HBAcceptor_allN)とを作ってみましょう!
import prolif as plf class HBAcceptor_allN(plf.interactions.HBAcceptor): def __init__(self): super().__init__(acceptor="[#7,O,F,-{1-};!+{1-}]")
元々のクラスを継承した新しいクラスを作成し、super()で親クラスの__init__メソッド実行時のパラメータを書き換えています*2
ここではアクセプターのSMARTSのNを#7に変更しました。
同様にして水素結合ドナー(prolif.interactions.HBDonor(donor='[#7,#8,#16][H]', acceptor='[N,O,F,-{1-};!+{1-}]', distance=3.5, angles=(130, 180)))についても新しいクラスを作っておきましょう。
class HBDonor_allN(plf.interactions.HBDonor): def __init__(self): super().__init__(acceptor="[#7,N,O,F,-{1-};!+{1-}]")
これらの新しい水素結合クラスを使って、ProLIFの水素結合認識範囲はひろがるでしょうか???
4-2-6. MDトラジェクトリの再解析
それではMDトラジェクトリをもう一度ProLIFで解析してみましょう。
まずはMDAnalysisで読み込んで解析の準備をします。
import MDAnalysis as mda from MDAnalysis.analysis import align # topology(.pdb)とtrajectory(.dcd)からUniverseオブジェクトを構築 md_universe = mda.Universe("complex_simulation_data/complex_prep.pdb", "complex_simulation_data/trajectory.dcd") # Cα原子でアラインメントを取る alignment = align.AlignTraj( mobile = md_universe, reference = md_universe, select="name CA", in_memory=True) alignment.run()
リガンドとタンパクを選択します。
# MDAnalysisでリガンドとタンパクを選択 lig = md_universe.atoms.select_atoms("resname LIG") prot = md_universe.atoms.select_atoms("protein")
新しくつくったProLIFの相互作用(['HBAcceptor_allN', 'HBDonor_allN'])を指定したFingerprintを作ります。
# 解析したい相互作用のFingerprint fp = plf.Fingerprint(['HBAcceptor_allN', 'HBDonor_allN']) # トラジェクトリを渡して解析実行 fp.run(md_universe.trajectory[::10], lig, prot, residues = "all") df_fp = fp.to_dataframe() df_fp

検出されたのは前回と同じくASP155との相互作用だけでした。解析対象をトラジェクトリの全フレームにしてもASP155以外は見つかりませんでした。
定義を変えてacceptorの窒素原子を全て(アリファティック以外も含む)に変更しても、目的のヒンジ領域との相互作用は検出できないようです。残念。
4-3. OpenMMからAmberのファイルに変換してMMPBSA
先にAmberToolsにはエネルギー計算(MMPB-SA.py)するためのツールがあると書きました。
Google検索しているとOpenMMで計算した結果をAmberの対応ファイルに変換してエネルギー計算しようとしている例などが出てきました。
そこでまずはファイル変換方法を試しました。
4-3-1. ParmEdのインストール
ファイルの変換ができるツールとしてParmEdがあります。(Making it rain でも使われていました)
インストールはcondaでOKです。
conda install -c conda-forge parmed
4-3-1. ParmEdのファイル変換でエラー
ParmEdでファイル変換を行うには、目的の構造をParmEdのStructureオブジェクトに変換したのち.save()で望みのファイル形式を選択します。
OpenMMからParmEdのStructureを作るには、load_fileで「①トポロジーと②系(SystemのXML)」を読み込みます。
import parmed as pmd # トポロジーのためにPDB読み込み test_pdb = pmd.load_file("complex_simulation_data/complex_prep.pdb") # OpenMMで作ったsystem.xml情報の読み込み test_system_xml = pmd.load_file("complex_simulation_data/system.xml") # ParmEdのStructure作成 test_struct = pmd.openmm.load_topology(test_pdb.topology, test_system_xml)
ところがこれをAmberのファイル形式(prmtop or parm7)に変換しようとするとエラーが出ました。
test_struct.save("test_amb.prmtop") """エラ-メッセージ 〜省略〜 1579 for bond in self.bonds: -> 1580 bond.type.used = True 1581 self.bond_types.prune_unused() 1582 data['BOND_FORCE_CONSTANT'] = [type.k for type in self.bond_types] AttributeError: 'NoneType' object has no attribute 'used' """
以上のように、「AttributeError: 'NoneType' object has no attribute 'used'」というエラーが出ます。bond_typeがNoneTypeになっているのがいけないようです。
4-3-2. エラーの原因と回避策
同様のエラーの報告例があり、回避策も2通りありました。
上記の議論によると、OpenMMでforcefieldからcreateSystemで系を構築する際に、拘束条件(constraints)が設定されているとbondのパラメータを消してしまうそうです。そのためParmEdがbond typeをアサインできずNoneのエラーになるとのこと。
回避策①として、createSystemの引数にflexibleConstraints=Trueを与えて系を構築する方法が挙げられていました。
例えば、Part 8で使ったコードを修正すると以下のようにします。
# flexibleConstraints=TrueでSystemをつくる system = FF.createSystem(complex_pdb.topology, nonbondedMethod=PME, nonbondedCutoff=1.0*unit.nanometers, constraints = HBonds, rigidWater=True, ewaldErrorTolerance=0.0005, flexibleConstraints=True) # SystemをXMLで出力する with open("flexConst_system.xml", mode="w") as file: file.write(XmlSerializer.serialize(system))
以上のようにして作成したSystemのXMLをParmEdで読み込んでみます。
# 作り直したSystemのxmlを読み込み test_system_xml2 = pmd.load_file("flexConst_system.xml") # ParmEdのStructure作成 test_struct2 = pmd.openmm.load_topology(test_pdb.topology, test_system_xml2) # Amber形式で出力 test_struct2.save("test_amb.prmtop")
作り直したSystemの情報を使うと無事「test_amb.prmtop」ファイルが作成されました!
また、OpenMMのSystemを作り直すのが面倒な場合、回避策②としてダミーのbond typeを割り当てる方法も挙げられていました。
# ダミーのbond typeを割り当てる bond_type = pmd.BondType(1.0, 1.0, list=test_struct.bond_types) test_struct.bond_types.append(bond_type) for bond in test_struct.bonds: if bond.type is None: bond.type = bond_type # Amber形式で出力 test_struct.save('bond_type_assinged.prmtop')
こちらの方法でも無事「bond_type_assinged.prmtop」ファイルが作成されました!
4-3-3. MMPB-SAの失敗
Amber形式にファイル変換する方法がわかったので、MMPB-SA計算ができるかどうかを試します。
計算に必要なファイルは複合体、タンパク質のみ、リガンドのみのトポロジーのようです。
そこで先のParmEdのStructureからそれぞれ必要な部分構造を抜き出して以下のようにファイルを作成しました。
# タンパク質を残基番号 1-317 で選択して出力 pmd_protein = test_struct[':1-317'] pmd_protein.save('protein.prmtop') # リガンドを残基名 LIG で選択して出力 pmd_ligand = test_struct[':LIG'] pmd_ligand.save('ligand.prmtop') # 複合体を出力 pmd_complex = test_struct[':1-317, LIG'] pmd_complex.save('complex.prmtop') print(pmd_protein) print(pmd_ligand) print(pmd_complex) # <Structure 5120 atoms; 317 residues; 5176 bonds; PBC (orthogonal); parametrized> # <Structure 63 atoms; 1 residues; 66 bonds; PBC (orthogonal); parametrized> # <Structure 5183 atoms; 318 residues; 5242 bonds; PBC (orthogonal); parametrized>
原子数を見る限り目的の構造を選択できていそうです。
これらのファイルを使って、Making it rainを参考にante-MMPBSA.py``MMPBSA.pyを使おうとしました。
ところが構造を作れないといったエラーがでてうまくいきませんでした。エラーの中身を見てもよくわかりませんでした。Amberの勉強をしないとわからなさそうです。。。
以上、試してうまくいかなかったこと2点でした。
5. おわりに
以上、今回は関連記事のまとめとMD計算を試した感想でした。また、失敗例は使い道はありませんが、検討中にわかったこと(ParmEdの使い方)もあったので備忘録として残しておきました。
Part 1から3ヶ月以上もかかってしまいましたが、素人のチュートリアルお試し記事にお付き合いいただきありがとうございました!
色々とご指摘・ご教示いただければ幸いです。
ではでは!
*1:参考:Daylight SMARTSの説明
*2:参考:ProLIF ドキュメント 2.1.2. Reparameterizing an interaction with another name
OpenMMをステップバイステップで 〜 Part 9 低分子-タンパク複合体のトラジェクトリ解析 〜
OpenMMの使い方を順番にたどる記事のPart 9です。
前回の記事(Part 8)では「低分子 - タンパク質複合体」についてシミュレーション系の構築と計算の実行を行いました。この記事では結果の解析を行います。
一般的な解析手法についてはPart 6、Part 7で確認しました。この記事では「低分子リガンドとタンパク質の相互作用解析」に焦点を当てたいと思います。
コードは基本的にTeachOpenCADD T020:Analyzing molecular dynamics simulationsとMaking it rain : Protein-Ligand smulationsからお借りしています。

1. キナーゼと阻害剤
具体的な解析を眺める前に、計算対象の構造の特徴について前提知識のおさらいをしておきます。
今回の構造はPDB ID: 3POZでEGFRタンパクのキナーゼドメインとリガンド TAK-285のX線共結晶構造です。
キナーゼは「ATPなどの高エネルギーリン酸結合を有する分子からリン酸基を基質あるいはターゲット分子に転移する(リン酸化する)酵素の総称」(Wikipedia - キナーゼ)です。なのでATP結合部位があることが多く、EGFRタンパクの場合以下のようなイメージになるでしょうか?*1

ATPのアデニンと水素結合を作っているのがヒンジ領域(Hinge region)と呼ばれる部分で、EGFRでは「Gln(Q) 791, Leu(L) 792, Met(M) 793」に相当します(あとで解析の際に残基番号を使います)。
キナーゼ阻害剤は結合様式によって分類され「ATP結合部位とその近縁のみ」に結合するものはType-Iと呼ばれるそうです。
木下誉富 キナーゼを標的とした構造生物学および創薬の現状 日本結晶学会誌 59,174-181(2017)
計算の対象としている複合体の構造では結合部位はこのようなイメージです(見やすさ重視で加工してます)。

アデニンに類似したピロロピリミジン環(?)がヒンジ領域のMet 793としっかり水素結合を作っていそうです。ただし、水素結合に関与しているピリミジン部位の窒素原子の位置は異なるようです。ATPとTAK-285の構造式を2次元でならべるとそっくりに見える部分構造でも、タンパク質との複合体では完全には重ならないというあたりに構造生物学の面白さを感じます。
なお、ピロロピリミジン環の先に伸びるフェニル環部分はEGFRポケットのゲートキーパー、疎水性ポケットへと伸びています。初期のキナーゼ阻害剤に対する獲得耐性変異としてT790Mなどが知られているそうです。確かに結合部位内で変異が起きてしまったらリガンドが結合しづらくなりそうですね。*2
ざっとですがキナーゼ阻害剤のおさらいは以上です。
2. 低分子 - タンパク質複合体のトラジェクトリ解析
2-1. トラジェクトリの動画
最初にPyMolで確認したトラジェクトリの動画を貼っておきます。(前回の記事の最後に貼ったもの)

リガンドが結構動いてますね。
2-2. MDAnalysisでRMSD解析
2-2-1. RMSDの推移
それでは具体的な解析を進めていきましょう!
まずはシミュレーションが崩壊していないかの確認も含めてトラジェクトリ全体のRMSDの推移を見てみます。
MDAnalysisを使うので、データを読み込んでUniverseオブジェクトを作成しアラインメントをとりましょう。
import MDAnalysis as mda from MDAnalysis.analysis import align # topology(.pdb)とtrajectory(.dcd)からUniverseオブジェクトを構築 md_universe = mda.Universe("complex_simulation_data/complex_prep.pdb", "complex_simulation_data/trajectory.dcd") # Cα原子でアラインメントを取る alignment = align.AlignTraj( mobile = md_universe, reference = md_universe, select="name CA", in_memory=True) alignment.run()
トラジェクトリ全体のRMSDはMDAnalysis.analysis.rms.RMSD()で確認できます。
今回は主鎖(backbone)のRMSDを取ると同時に、タンパク質全体(protein)とリガンド(resname LIG)も追加で計算します。*3
追加の計算対象は「引数 groupselections」で指定します。selectで選んだメインのAtomGroupについて重ね合わせた状態で、追加のAtomGroupについて計算が行われます。
from MDAnalysis.analysis import rms # フレームのリセット md_universe.trajectory[0] # RMSD解析(メイン "backbone", 追加 ["protein", "resname LIG"]) RMSD_analysis = rms.RMSD(md_universe, reference = md_universe, select = "backbone", groupselections = ["protein", "resname LIG"], ref_frame=0) RMSD_analysis.run()
結果をプロットしましょう。
results.rmsdに「[[frame, time(ps), RMSD(A), RMSD(A), RMSD(A)], [...], [...]]」形式で入っているので、PandasのDataFrameにしてからmatplotlibでプロットします。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns # 結果のDataFrameへの変換 column_names = ['frame', 'time(ps)', 'backbone', 'protein', 'ligand'] rmsd_df = pd.DataFrame(np.round(RMSD_analysis.results.rmsd, 2), columns = column_names) # 結果のプロット plt.plot(rmsd_df['time(ps)'], rmsd_df['backbone'], label="backbone") plt.plot(rmsd_df['time(ps)'], rmsd_df['protein'], label="protein") plt.plot(rmsd_df['time(ps)'], rmsd_df['ligand'], label="ligand") plt.legend(loc="upper left") plt.xlabel("Time (ps)") plt.ylabel("RMSD [$\AA$]") plt.title("RMSD of protein and ligand") plt.show()

主鎖が青色、タンパク全体がオレンジ色、リガンドが緑色です。タンパク質に比べるとリガンドの振れ幅が大きいですね。ただし、これはbackbone基準で合わせた場合なので、リガンドだけを考慮した場合とは異なることにご注意ください。
2-2-2. フレーム間のRMSD
先に見たRMSDは最初のフレーム(トラジェクトリ 0 ps)に対するものだったので、フレーム間のペアワイズのRMSDを見てみましょう。diffusionmap.Distancematrixを使います。
from MDAnalysis.analysis import diffusionmap # proteinについてペアワイズRMSDを計算 pairwase_protein = diffusionmap.DistanceMatrix(md_universe, select = "protein") pairwase_protein.run() dist_matrix_protein = pairwase_protein.results.dist_matrix # ligandについてペアワイズRMSDを計算 pairwase_ligand = diffusionmap.DistanceMatrix(md_universe, select = "resname LIG") pairwase_ligand.run() dist_matrix_ligand = pairwase_ligand.results.dist_matrix
結果は2Dのマトリックスです(ndarray)。ヒートマップで可視化しましょう!
proteinとligandでヒートマップの色のレンジを合わせるため、最初にフレーム間の距離の最大値をとっておいてvmaxに指定します。
# コードはTeachOpenCADD T20より # フレーム間の距離の最大値を取得(heatmapのvmaxに使用) max_dist = max(np.amax(dist_matrix_ligand), np.amax(dist_matrix_protein)) # プロットを作成 fig, ax = plt.subplots(1, 2) fig.suptitle("RMSD between the frames") # タンパクについてsubplot img1 = ax[0].imshow(dist_matrix_protein, cmap="viridis", vmin=0, vmax=max_dist) ax[0].title.set_text("protein") ax[0].set_xlabel("frames") ax[0].set_ylabel("frames") # リガンドについてsubplot img2 = ax[1].imshow(dist_matrix_ligand, cmap="viridis", vmin=0, vmax=max_dist) ax[1].title.set_text("Ligand") ax[1].set_xlabel("frames") fig.colorbar(img1, ax=ax, orientation="horizontal", fraction=0.1, label="RMSD (Å)")

タンパク質のRMSDは時間推移で近いフレーム間では小さく、離れたフレーム間では大きくなっているようです。時間発展に伴って少しづつ全体の構造が変わっているようですね。
対して、リガンドではフレームが離れた箇所でもペアワイズのRMSDが小さくなる部分がありました。時間経過のプロットでも大きくRMSDが動いている箇所があったので、一定の範囲内で構造の揺り戻しが起きているのかもしれません。
2-3. Protein-Ligand Interaction Fingerprint(ProLIF)で相互作用解析
2-3-1. ProLIF?
つづいて具体的に「どの残基がリガンドと相互作用をしているか?」解析したいと思います。
ここではProLIF(Protein-Ligand Interaction Fingerprints)というツールを使います。タンパク質とリガンドとの相互作用をフィンガープリント形式にして解析してくれる素敵なツールです。
- 論文:Bouysset, C., Fiorucci, S. ProLIF: a library to encode molecular interactions as fingerprints. J Cheminform 13, 72 (2021).
- ProLIF GitHub
- ProLIF Documentation
ProLIFとは別のツールで恐縮ですが、動作のイメージをつかむためにPLIP(Protein-Ligand Interaction Profiler)の解析図を貼っておきます。*4

上図のようにPLIPではタンパク質とリガンド間にある(非共有結合の)相互作用を種類別に分けて解析してくれます。「ある残基との間にある種類の相互作用が有るか?無いか?」をフィンガープリントとして捉えるというイメージです。
PLIPの入力はPDBファイルで1点の静止画ですが、ProLIFを使うとMDトラジェクトリ(動画)を対象とした解析ができます。
ProLIFのインストールにはいくつか必要なライブラリがあります。ドキュメントのInstallationを参考にインストールしましょう。
推奨はcondaで専用の仮想環境を作った上で、githubからpipでインストールするみたいです。
# 仮想環境を作る conda create -n prolif # 仮想環境のアクティベート conda activate prolif # 主な依存ライブラリのインストール(これら以外は自動でインストールされる) conda config --add channels conda-forge conda install rdkit cython # ProLIFのインストール pip install git+https://github.com/chemosim-lab/ProLIF.git
※ 注意 「pip install prolif」は使えないそうです。
私はMDお試し用の仮想環境に上記でインストールしました。
2-3-2. ProLIFでフィンガープリント解析
それではProLIFで相互作用フィンガープリントを解析してみましょう。
ProLIFはMDAnalysisで読み込んだトラジェクトリを対象として解析できます。リガンドおよびタンパク質の指定が必要なのでMDAnalysisでslect_atomsしてからProLIFのFingerprintを使いましょう。
import prolif as plf # MDAnalysisでリガンドとタンパクを選択 lig = md_universe.atoms.select_atoms("resname LIG") prot = md_universe.atoms.select_atoms("protein") # デフォルトの相互作用解析 fp = plf.Fingerprint() # トラジェクトリを渡して解析実行 fp.run(md_universe.trajectory[::10], lig, prot)
上記はトラジェクトリを10フレームごとに解析する場合です(スライスで指定)。今回は50フレームのトラジェクトリなので5セットの結果が出ます。
デフォルトではリガンドの周囲6.0Åの範囲にある残基を対象として解析を行います。
結果はPandasのDataFrameに出力することができます。
df_fp = fp.to_dataframe() df_fp

ProLIFのデフォルトの解析で見つかった相互作用(True)は「0フレーム目でASP155.Aが水素結合ドナー(HBDonor)」として働いているというもののみでした。残りのフレーム、また他の残基との間に相互作用は検出できなかったようです。
今回のシミュレーション構造は「残基番号 700 〜 1017」なのでASP155.Aは「鎖AのD855」に相当します。ちょうどDFGループのDですね。
期待していたのはヒンジ領域(QLM)との相互作用でしたが出なかったものは仕方ない...残念。
2-3-3. ProLIFでLigand Interaction Network(LigPlot)
DataFrameのみだと味気ないのでもう少し凝った描画をしてみましょう。
ProLIFのLigNetworkを使うと、LigProtのようなお洒落な2Dダイアグラムが作成できます。
引数にはProLIFの「① 相互作用フィンガープリント解析結果(ifp)のデータフレーム」と「②リガンドをMoleculeオブジェクトにしたもの」を渡します。ただし、データフレーム(①)は「引数return_atoms=True」を設定している必要があるのでもう一度作り直しています。
from prolif.plotting.network import LigNetwork # ① LigPlot用のifpのDataFrame df_lpt = fp.to_dataframe(return_atoms = True) # ② リガンドをMDAnalysisのオブジェクトからProLIFのMoleculeオブジェクトにしておく lmol = plf.Molecule.from_mda(lig) # ifpのDataFrameから2Dネットワークを作成 # フレーム 0から2D描画を作る場合 net = LigNetwork.from_ifp(df_lpt, lmol, kind='frame', frame=0) net.display()

できました!アスパラギン酸(ASP155)の酸性側鎖とリガンド(TAK-285)の水酸基との間に水素結合ができているようです。シンプルでみやすいですね。
今回は最初のfram 0でのみ相互作用が検出(True)されていたので LigNetwork.from_ifpの「引数 kind='frame', frame=0」としました。
全てのフレームを合算した結果を描画したい時は「kind='aggregate'」とすればOKです。また、「threshold=0.3」とすれば合算した3割以上(閾値 0.3以上)の割合で見えている相互作用に限定して描画することもできます。
ちなみにPyMolでトラジェクトリの最初の方を確認するとこんな感じです。

ヒンジ領域も結構近いのに検出してくれないのかー。厳しい。。。*5
以上でProLIFを使った解析はおしまいです。
2-4. MDAnalysisで原子間距離の解析
つづいてMDAnalysisを使ってもう少し細かい解析を行いましょう。ProLIFで全体をざっとみただけでは拾いきれなかったものが見えるかもしれません。
まずは原子間距離を測ってみたいと思います。
シミュレーション時にリガンドの各原子につけた名前は以下のようになっています。

また、タンパク質は以下のように前処理をしているため、シミュレーション上の残基の番号は元の構造と700ずれます。

MDAnalysisでは各原子を「残基ID(resid) or 残基名(resname)」と「原子の名前(name)」の組み合わせで指定することができます(select_atoms)。
先の注意点を踏まえると「Met 793(→resid 93)の主鎖N原子」と「リガンド(resname LIG)のN4」は以下のように指定できます。
# EGFRのMet793のN atomgroup_M793N = md_universe.select_atoms("resid 93 and name N") # LigandのN4 atomgroup_LIG_N4 = md_universe.select_atoms("resname LIG and name N4")
この2原子の距離はdistances.distを使って求められます。
from MDAnalysis.analysis import distances dist_M793N_LigN4 = distances.dist(atomgroup_M793N, atomgroup_LIG_N4) print(dist_M793N_LigN4) # [[93. ] # [ 1. ] # [ 3.30475404]]
戻り値はnumpy.ndarrayで「[[一つ目のAtomGroupの残基ID], [2つ目のAtomGroupの残基ID], [原子間距離(Å)]] 」となっています。
従ってMet残基とリガンドN4原子の距離は3.3Åとなります。トラジェクトリに沿った変化を眺めてみましょう。
# トラジェクトリの各フレームごとに原子間距離を求めてリストに格納 distlist_M793N_LigN4 = [] for _ in md_universe.trajectory: dist_t = distances.dist(atomgroup_M793N, atomgroup_LIG_N4)[2][0] distlist_M793N_LigN4.append(dist_t) # 最小値、最大値 print("shortest length(A) : ", np.round(min(distlist_M793N_LigN4), 2)) print("longest length(A) : ", np.round(max(distlist_M793N_LigN4), 2)) # プロット plt.plot(distlist_M793N_LigN4) plt.ylabel("distance (Å)") plt.xlabel("frame") plt.ylim(0.0, 4.0) plt.title("Distance between Met793's N and LIG's N4") plt.show() # shortest length(A) : 2.92 # longest length(A) : 3.92

全体では「2.9Å〜 3.9Å」の範囲を行ったり来たりしているようです。
ちょっと長めですが最小値周りでは水素結合を形成する距離に入っていると言って良いかもしれません。
ところでこういう場合、結晶構造の分解能(PDB ID : 3POZ, Resolution: 1.50 Å)はどう考慮すれば良いのでしょうか?MD計算したから解消されていると考えるのか?計算後も誤差として分解能を考慮すべきか?・・・よくわかりません。ご教示いただけると嬉しいです。
2-5. MDAnalysisで水素結合の解析-1
さて、原子間距離の解析はできましたが水素結合を考慮するには角度も合わせて考える必要があります。
MDAnalysisには水素結合解析の機能も用意されています(hydrogenbonds.hbond_analysis))。
設定する引数が多いですが1つ1つはシンプルです。
- ① ドナー(D)原子(
donors_sel(str)) - ② 水素原子(H)本体(
hydrogens_sel(str)) - ③ アクセプター(A)原子(
acceptors_sel(str)) - ④ ドナーと水素原子(D-H)のカットオフ距離(
d_h_cutoff(float)、デフォルト 1.2) - ⑤ ドナーとアクセプター(D-A)のカットオフ距離(
d_a_cutoff(float)、デフォルト 3.0) - ⑥ ドナー - 水素 - アクセプター(D-H-A)の角度(
d_h_a_angle_cutoff、デフォルト 150)
水素結合の定義そのものという感じですね。
それではドナーを「Met 793(→resid 93)の主鎖N原子」、アクセプターを「リガンド(resname LIG)のN4」として解析してみましょう。
from MDAnalysis.analysis.hydrogenbonds import hbond_analysis # ① ドナー原子 donor_MetN = "resid 93 and name N" # ② 水素原子 donor_MetH = "resid 93 and name H" # ③ アクセプター原子 acceptor_LigN = "resname LIG and name N4" hb_analyzer = hbond_analysis.HydrogenBondAnalysis(md_universe, donors_sel = donor_MetN, hydrogens_sel = donor_MetH, acceptors_sel = acceptor_LigN, d_h_cutoff = 1.2, d_a_cutoff = 3.0, d_h_a_angle_cutoff = 150) hb_analyzer.run()
結果はresults.hbondsにnumpy.ndarrayとして格納されていて「[<frame>, <donor atom id>, <hydrogen atom id>, <acceptor atom id>, <distance>, <angle>] 」となっています。
DataFrameに変換しましょう。
column_names = ["frame", "donor_index", "hydrogen_index", "acceptor_index", "distance", "angle"] hb_anal_df =pd.DataFrame(np.round(hb_analyzer.results.hbonds, 2), columns = column_names) hb_anal_df.set_index("frame")

全50フレームのうち4フレームでのみ(デフォルトの)水素結合形成条件を満たしました。1割以下なのでProLIFで検出されなかったのも仕方ないかもしれませんね。
このままプロットしてもつまらないのでカットオフを緩めて再解析してみましょう(d_a_cutoff = 3.5)。解析結果のD-A距離とD-H-A角度は一つのプロットにまとめて描画します。
# ドナー - アクセプター カットオフ距離を3.5にして再解析 hb_analyzer_35 = hbond_analysis.HydrogenBondAnalysis(md_universe, donors_sel = donor_MetN, hydrogens_sel = donor_MetH, acceptors_sel = acceptor_LigN, d_h_cutoff = 1.2, d_a_cutoff = 3.5, d_h_a_angle_cutoff = 150) hb_analyzer_35.run() # DataFrame化 hb_anal_df_35 =pd.DataFrame(np.round(hb_analyzer_35.results.hbonds, 2), columns = column_names) hb_anal_df_35.set_index("frame") # プロットを作成 fig = plt.figure(figsize=(10, 6)) dist_plot = hb_anal_df_35["distance"].plot(style="o", x="frame") dist_plot.set_ylabel("distance (Å)") dist_plot.set_xlabel("frame") dist_plot.set_ylim(0.0, 4.0) angle_plot = hb_anal_df_35["angle"].plot(secondary_y=True, style="*", x="frame") angle_plot .set_ylabel("angle (°)") angle_plot .set_xlabel("frame") angle_plot .set_ylim(0.0, 180) fig.legend(loc="lower right", bbox_to_anchor=(1, 0), bbox_transform=dist_plot.transAxes) plt.show()

D-A距離(distance)とD-H-A角度(angle)は一見連動して動いているように見えますが所々逆の動き(short length & wide angle)になっているのが面白いですね。
TeachOpenCADD T20では同様の解析を経て、距離のばらつきに対して角度は180度近くで安定化していることからリガンドの結合に重要な相互作用となっているのではないかと考察されていました。・・・なるほど、そう解釈するのか!
2-6. MDAnalysisで水素結合の解析-2
MDAnalysisによる水素結合解析の方法がわかったので、ProLIFで見つかった「ASP 855(→resid 155)の側鎖OD1/OD2原子」と「リガンド(resname LIG)のO3」との相互作用も解析してみましょう。
コードは同じことの繰り返しですが、アスパラギン酸側鎖のカルボキシ基には酸素原子が2つあるので両者で違いがでるか?興味があります。
水素結合のカットオフを緩めて解析してみました(d_a_cutoff = 4.0, d_h_a_angle_cutoff = 120)。
# ① ドナー原子 donor_LigO = "resname LIG and name O3" # ② 水素原子 donor_LigH = "resname LIG and name H22" # ③ アクセプター原子−1 acceptor_AspOD1 = "resid 155 and name OD1" # ③ アクセプター原子−2 acceptor_AspOD2 = "resid 155 and name OD2" # Asp OD1原子について解析 hb_analyzer_OD1 = hbond_analysis.HydrogenBondAnalysis(md_universe, donors_sel = donor_LigO, hydrogens_sel = donor_LigH, acceptors_sel = acceptor_AspOD1, d_h_cutoff = 1.2, d_a_cutoff = 4.0, d_h_a_angle_cutoff = 120) hb_analyzer_OD1.run() # Asp OD1原子の解析結果データフレーム hb_anal_OD1_df =pd.DataFrame(np.round(hb_analyzer_OD1.results.hbonds, 2), columns = column_names) # Asp OD2原子について解析 hb_analyzer_OD2 = hbond_analysis.HydrogenBondAnalysis(md_universe, donors_sel = donor_LigO, hydrogens_sel = donor_LigH, acceptors_sel = acceptor_AspOD2, d_h_cutoff = 1.2, d_a_cutoff = 4.0, d_h_a_angle_cutoff = 120) hb_analyzer_OD2.run() # Asp OD2原子の解析結果データフレーム hb_anal_OD2_df =pd.DataFrame(np.round(hb_analyzer_OD2.results.hbonds, 2), columns = column_names)
まずはD-A距離についてAspの2つの酸素原子(OD1/OD2)の結果を一緒にプロットしてみましょう。
# D-A距離についてOD1/OD2を同時にプロット plt.scatter(hb_anal_OD1_df["frame"], hb_anal_OD1_df["distance"], color = 'red', marker="o", label="with OD1") plt.scatter(hb_anal_OD2_df["frame"], hb_anal_OD2_df["distance"], color = 'blue', marker="*", label="with OD2") plt.xlabel("frame") plt.ylabel("distance (Å)") plt.ylim(0.0, 4.0) plt.legend() plt.show()

Asp855側鎖のカルボキシ基のうち、OD2原子(red circle)はリガンド水酸基と4.0Åの距離に入ったのは3/50フレームのみでいずれもギリギリ4.0以下でした。
一方で、OD1原子(blue star)は26/50フレームで4.0Å以下の距離に入り、3.0Å以下の点も多くみられます。
同様にD-H-A角度についてもプロットしてみましょう。
# D-H-A角度についてOD1/OD2を同時にプロット plt.scatter(hb_anal_OD1_df["frame"], hb_anal_OD1_df["angle"], color = 'red', marker="o", label="with OD1") plt.scatter(hb_anal_OD2_df["frame"], hb_anal_OD2_df["angle"], color = 'blue', marker="*", label="with OD2") plt.xlabel("frame") plt.ylabel("angle (°)") plt.ylim(0, 180) plt.legend() plt.show()

角度についても、OD2原子(red circle)は3フレームとも150°よりも小さく、水素結合の基準を満たしそうにありませんでした。
また、OD1原子(blue star)も半数近くは150°以下となっており、距離、角度ともに基準を満たすものは10フレーム前後(2割程度)に落ち着きそう、という結果になりました。
以上の比較から、今回の複合体トラジェクトリではAsp855側鎖カルボキシ基の一方の酸素原子(OD2)とは水素結合を形成するものの、もう一方の酸素原子(OD1)に結合が切り替わることは観察されませんでした。
もう少しつっこむと、30フレーム(600 ps)以降では距離、角度ともに(デフォルトの)水素結合要件を満たすものはありませんでした。つまり、1nsの短いシミュレーションの初期でたまたま見られた偶然の結合の可能性もあります。
ご参考までに計算対象の元のPDB(3POZ)の構造を貼っておきます。

PyMolのデフォルトではリガンド(TAK-285)の水酸基はArg841の主鎖カルボニル酸素およびAsn842の側鎖アミドカルボニル酸素と相互作用しています。一方、タンパク(EGFR)のAsp855はK745と水分子を介したネットワークを形成しているようです。
この共結晶構造解析だけからリガンド OH基とタンパクのAsp855が水素結合を形成する可能性を考慮するのは難しそうです。今回のMDシミュレーションで見られた相互作用をランダムに与えられた初速の産んだ偶然と捉えるか?、X線共結晶では捉えられなかった相互作用と捉えるか?、繰り返しのMDシミュレーションやより長時間のシミュレーションを行えばわかるのかもしれませんが、私の手には負えません。。。。
3. おわりに
以上、今回は低分子ータンパク複合体のMDシミュレーションについてトラジェクトリ解析を試してみました。
特に(イメージしやすい古典的な)水素結合形成の解析に焦点を当てて、ProLIFやMDAnalysisを使った解析を追いかけてみました。・・・といってもほとんどTeachOpenCADD T20とMaking it rainのコードのCopy&Pasteですが。。。
個人的にはProLIFの解析で当初想定していたリガンド TAK-285とタンパク Hinge領域との相互作用が検出できなかったものの、もともとの共結晶構造(PDB ID:3POZ)を眺めるだけでは想像し難いリガンド OH基とタンパク D855 側鎖カルボキシ基との間に水素結合を形成する可能性が示唆された点が非常に興味深かったです。
・・・といっても、MD計算で初期に与えるランダムな速度分布の偶然の結果かもしれません。
より突っ込んだ解析、考察は門外漢の私には手に余るので専門家の皆様にお任せします(丸投げ)。
「MD計算の解釈で元の構造の分解能をどう考慮すれば良いか?」など、色々とわからないことが多かったです。今回も間違いが多いと思うのでご指摘をいただければ幸いです。
ではでは!
*1:PDB ID: 2TIXのリガンドは正確にはATPそのものではなくアナログの「Phosphoaminophosphonic acid-adenylate ester(ANP)」と呼ばれるものです。あくまでイメージとしてご容赦ください。
*2:Structure Based Drug DesignでTAK-285をベースにした構造から展開し、T790M/L858R変異に対しても活性を有する化合物を得る文献もありました。ACS Med Chem Lett. 2012(4)201。PubMedで読めます。
*3:リガンドの名前(LIG)は前回シミュレーション系構築の際につけました
*4:PLIPの文献はこちら Melissa F Adasme, Katja L Linnemann, Sarah Naomi Bolz, Florian Kaiser, Sebastian Salentin, V Joachim Haupt, Michael Schroeder, PLIP 2021: expanding the scope of the protein–ligand interaction profiler to DNA and RNA, Nucleic Acids Research, Volume 49, Issue W1, 2 July 2021, Pages W530–W534,
*5:なお、ProLIFはトラジェクトリ以外のデータも解析できます。Fingerprintオブジェクトを作成後、run()ではなくgenerate()を使えば1対1、run_from_iterable()を使えば複数を対象にした解析ができます。ドッキングの結果の複合体に対して適用したりすることができるようです。参考:Working with docking poses instead of MD simulations
